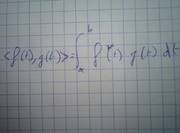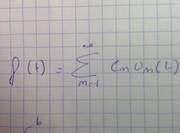I Components of functions in vector spaces

[DoobleD]

I have some conceptual issues with functions in vectors spaces. I don't really get what are really the components of the vector / function.

When we look at the inner product, it's very similar to dot product, as if each value of a function was a component :

So I tend to think to f(t) as the vector whose components are : (f(1), f(2), ..., f(n)).

But a function can also be approximated as a series of some constants times a base function from an orthonormal set spaning the space. Quite like a vector in 3D for instance, with constants times unit vectors, but with possibly an infinity of dimensions, and base functions instead of unit vectors. Like so (Cn is a constant, Un is a base function) :

Then I'm like : uh, so, what are the vector-like components of a function ? Are they the values of the function, f(t), or the constants Cn ? Which one is it ? It can't be both (I think) because those are simply not the same thing. f(3) != C3.

 

[Stephen Tashi]

I have some conceptual issues with functions in vectors spaces.

I think you mean "a function considered as a vector in a infinite dimensional space".

When we look at the inner product, it's very similar to dot product, as if each value of a function was a component :

So I tend to think to f(t) as the vector whose components are : (f(1), f(2), ..., f(n)).

That's an intuitive way to think about it.

Suppose $f(x) = a_1 e_1(x) + a_2 e_2(x)$ and $g(x) = b_1 e_1(x) + b_2 e_2(x)$.

Compute the inner product according the integral interpretation:
$\int f(x) g(x) = \int ( a_1 e_1(x) + a_2 e_2(x))(b_1 e_1(x) + b_2 e_2(x))$
$= a_1 b_1 \int e_1(x) e_1(x) + a_1 b_2 \int e_1(x) e_2(x) + a_2 b_1\int e_2(x) e_1(x) + a_2 b_2 \int e_2(x) e_2(x)$

If we want that result to be consistent the the coefficient interpretation: $a_1 b_1 + a_2 b_2$ then it would be sufficient if $\int e_1(x) e_1(x) = 1 = \int e_2(x) e_2(x)$ and $\int e_1(x) e_2(x) = 0 = \int e_2(x) e_1(x)$.

Those conditions apply if $e_1(x), e_2(x)$ are an orthonormal basis with respect the integral interpretation of the inner product. So the integral interpretation is consistent with the coefficient interpretation provided you express functions as linear combinations of orthonormal basis functions. (The coefficient formula for the inner product in finite dimensional vectors spaces also assumes the vectors are expressed in an orthonormal basis.)

 

[DoobleD]

Thank you. I'm ok with the fact the integral works out to the sum of the multiplied coefficients, in this case : a1*b1 + a2*b2.

What bugs me is that if f(x) has components a1 and b1, then my intuitive way of thinking to f(x) as having components f(1), f(2), ..., f(n) is wrong.

a1*e1(x) + a2*e2(x) isn't equal to (f1)*e1(x) + f(2)*e2(x) + ... + f(n)*en(x).

What am I thinking the wrong way ?

 

[Stephen Tashi]

a1*e1(x) + a2*e2(x) isn't equal to (f1)*e1(x) + f(2)*e2(x) + ... + f(n)*en(x).

Think of $e_1(x)$ as the vector $( e_1(1), e_1(2), e_1(3),... )$ and $e_2(x)$ as the vector $(e_2(1),e_2(2),e_2(3),...)$

The vectors $e_i$ don't necessarily correspond to the "standard" unit vectors {(1,0,0..), (0,1,0,0),(0,0,1,0,..) } so the i_th component of $f$ isn't necessarily equal to the coefficient of the i_th unit vector when $f$ is expanded in an arbitrary basis. The same is true in finite dimensional vector spaces. If vector $F = aB + bC$ we don't know that the first component of $F$ is equal to $a$, even if $B$ and $C$ are orthonormal to each other. When each of $F,B,C$ are expressed in the same basis then we can infer a relation between the coefficients in the expansion and values of individual components.

 

[Mark44]

What bugs me is that if f(x) has components a1 and b1, then my intuitive way of thinking to f(x) as having components f(1), f(2), ..., f(n) is wrong.

The components of a function f, seen as an element of a function space (a kind of vector space) would be the basic functions that add up to f. The components wouldn't be f(1), f(2), and so on.

What I'm calling the "basic functions" form what is called a basis for the function space. A Maclaurin series decomposes a function into a linear combination of the basis functions {1, x, x², ... }. A Fourier series decomposes a function into a llinear combination of a different set of functions {sin(x), sin(2x), sin(3x), ..., cos(x), cos(2x), cos(3x), ... }.

 

[DoobleD]

Think of e1(x)e1(x) e_1(x) as the vector (e1(1),e1(2),e1(3),...)(e1(1),e1(2),e1(3),...)( e_1(1), e_1(2), e_1(3),... ) and e2(x)e2(x)e_2(x) as the vector (e2(1),e2(2),e2(3),...)(e2(1),e2(2),e2(3),...)(e_2(1),e_2(2),e_2(3),...)

The vectors eieie_i don't necessarily correspond to the "standard" unit vectors {(1,0,0..), (0,1,0,0),(0,0,1,0,..) } so the i_th component of fff isn't necessarily equal to the coefficient of the i_th unit vector when fff is expanded in an arbitrary basis. The same is true in finite dimensional vector spaces. If vector F=aB+bCF=aB+bCF = aB + bC we don't know that the first component of FFF is equal to aaa, even if BBB and CCC are orthonormal to each other. When each of F,B,CF,B,CF,B,C are expressed in the same basis then we can infer a relation between the coefficients in the expansion and values of individual components.

Ahh that makes sense ! I was going to ask then if f(1), f(2) etc. are the components of the "unitary" basis (1, 0, 0, ...), (0, 1, 0, ...), an so on (not necessarily in that order, f(-3) could be component of say the unit vector (0, 1, 0, ...)). But @Mark44 answered f(1), f(2), ... are not components :

The components of a function f, seen as an element of a function space (a kind of vector space) would be the basic functions that add up to f. The components wouldn't be f(1), f(2), and so on.

Then, why would the inner product be defined the way it is ? The inner product of f and g is an infinite sum of f(1)g(1) + f(2)g(2) + ... . And I thought the inner product was the analog of the dot product, which is, for vectors A and B, a sum of a1b1 + a2b2 + ..., with a1, b1, a2, b2, ... components of the vectors A and B.

So, the computation of both operations is the same, and the inner product is a generalization of the dot product, but somehow in the case of inner product, what the operation multiplies are not vector-like components ? I'm lost in this, I thought the inner product was basically a dot product but with an infinite amount of components...

 

[Stephen Tashi]

Ahh that makes sense ! I was going to ask then if f(1), f(2) etc. are the components of the "unitary" basis (1, 0, 0, ...), (0, 1, 0, ...), an so on (not necessarily in that order, f(-3) could be component of say the unit vector (0, 1, 0, ...)). But @Mark44 answered f(1), f(2), ... are not components :

We can discuss some technicalities. First, there is the basic question "Is a component of a vector also a vector?"

In a physics textbook, one sees vectors "resolved" into components, which are themselves vectors. In another textbook, we might see a "component" of vector defined as the coefficient that appears when we express a vector as the sum of basis vectors. So if $V = a1 E_1 + a2 E_2$ with $V,E_1,E_2$ vectors and $a1,a2$ scalars, what are the "components" of $V$ ? Are they $a1,a2$ or are they $a1 E_1, a2 E_2$ ? And if $V$ is represented as an ordered tuple $(a1,a2)$ is the "a1" in this representation taken to mean precisely the scalar a1 or is it a short hand notation for $a1 E_1$?

I don't have any axe to grind on those questions of terminology. I'll go along with the prevailing winds. But, for the moment, let's take the outlook of a physics textbook and speak of the "components" of a vector as being vectors. Suppose we want to resolve a function (considered as a vector) into other vectors. The notation "f(1)" denotes a real number, not a function. So you can't resolve a function (regarded as a vector) into a sum of other functions (regarded as vectors) only by using a set of scalars f(1),f(2),... To resolve f into other function, we can adopt the convention that "(f(1), f(2),f(3),...)" represents a sum of vectors. To do that we can define "f(k)" to denote the scalar f(k) times the function $e_k(x)$ where $e_k(x)$ is defined by: $e_k(x) = 1$ when $x = k$ and $e_k(x) = 0$ otherwise.

If you express f(x) as sum of functions defined by sines and cosines, then you are not using the functions $e_k(x)$ as the basis functions. So there is no reason to expect that a scalar such as f(1) has anything to do with the coefficients that appear when you expand f as sum of sines and cosines.

The dot product formula for the inner product assumes the two vectors being "dotted" are represented in the same orthonormal basis.

Then, why would the inner product be defined the way it is ? The inner product of f and g is an infinite sum of f(1)g(1) + f(2)g(2) + ... .

That's an intuitive way to think about it. To make a better analogy to the actual definition as in integral, you should put some dx's in that expression, unless you are talking about functions defined only on the natural numbers.

And I thought the inner product was the analog of the dot product, which is, for vectors A and B, a sum of a1b1 + a2b2 + ..., with a1, b1, a2, b2, ... components of the vectors A and B.

You are correct that (intuitively) the inner product (when defined as an integral) is an analogy to the dot product formula for vectors (which assumes the two vectors are represented in the same orthonormal basis).

Some mathematical technicalities are:

1) In pure mathematics, an inner product (not "the" inner product) has a abstract definition. It isn't defined by a formula.

2) The connection between the inner product on a vector space and the vectors is that the inner product is used to compute the "norm" of a vector (e.g. its "length").

3) In pure mathematics, vectors don't necessarily have a "norm". The abstract definition of a "vector space" doesn't require that vectors have a length. On the same vector space, it may be possible to define different "norms". (In the case of vector spaces of functions, we often see different norms defined.)

4) The set of scalars in a vector space isn't necessarily the set of real numbers. When we use the set of complex numbers as the scalars then we encounter a formula for a dot product that involves taking complex conjugates.

So, the computation of both operations is the same, and the inner product is a generalization of the dot product, but somehow in the case of inner product, what the operation multiplies are not vector-like components ?

The dot product formula doesn't multiply together "vector like components". It involves the multiplication of scalars.

You could write a formula for the dot product of two sums of vectors that involves the sum of dot-products of vectors. Is that what you mean by multiplying vector like components ?

 

[Mark44]

The components of a function f, seen as an element of a function space (a kind of vector space) would be the basic functions that add up to f. The components wouldn't be f(1), f(2), and so on.

Then, why would the inner product be defined the way it is ? The inner product of f and g is an infinite sum of f(1)g(1) + f(2)g(2) + ... .

No, not quite. For functions f and g it would be $\int_a^b fg~dt$, over some interval [a, b] that depends on the functions, but this is not the same as what you wrote (f(1)g(1) + f(2)g(2) + ...).

If $\vec{u}$ and $\vec{v}$ are complex vectors in $\mathbb{C}^n$, then $<\vec{u}, \vec{v}> = \sum_{i = 1}^n u_i \bar{v_i} = u_1\bar{v_1} + \dots + u_n\bar{v_n}$.

And I thought the inner product was the analog of the dot product

The dot product is one kind of inner product.

, which is, for vectors A and B, a sum of a1b1 + a2b2 + ..., with a1, b1, a2, b2, ... components of the vectors A and B.

So, the computation of both operations is the same

Similar, but not the same.

, and the inner product is a generalization of the dot product, but somehow in the case of inner product, what the operation multiplies are not vector-like components ? I'm lost in this, I thought the inner product was basically a dot product but with an infinite amount of components...

Maybe a couple of simple examples might help out here.

1. Vector space R²
One basis is u = <1, 1>, v = <1, -1>. Since these vectors have different directions, they are linearly independent, and since there are two of them, they form a basis for R² that I'll call B. That means that any vector in R² can be written as a linear combination of u and v. For example, the vector w = <5, 0> = (5/2)u + (5/2>v. The components of w, in terms of the basis {u, v} are 5/2 and 5/2. So we could write w_B as <5/2, 5/2>, showing the coordinates of this vector in terms of the basis B.

2. Function space p₂ (the space of polynomials of degree less than 2.
The standard basis for the space p₂ is {1, t}, but any two functions of degree less than 2 that are linearly independent also form a basis, such as 1 + t and 1 - t. I'll call this basis B. The function 5t can be written as (5/2)(1 + t) + (-5/2)(1 - t), so the "coordinates" of 5t in terms of the basis b are <5/2, -5/2>.

When you're working with the inner product of a function space, the coordinates of a function aren't f(1), f(2), and so on -- the coordinates are the constants that multiply each element of a some basis for that space.

Hope this helps.

 

[DoobleD]

Thank you for the help.

The dot product formula doesn't multiply together "vector like components". It involves the multiplication of scalars.

You could write a formula for the dot product of two sums of vectors that involves the sum of dot-products of vectors. Is that what you mean by multiplying vector like components ?

Sorry for the bad wording, english is not my native language so sometimes I might not be very clear. I understand all of what you wrote. Especially the fact that a vector coordinate in space (the scalar quantity I call a "component") depends of the chosen base functions (or unit vectors in Euclidian space). This does makes sense of course, and explains at least why f(1), f(2), ..., f(n) are not (necessarily?) the same as the components of, say, a Fourier series representing the same function. The Fourier series expresses the function with another set of basis functions, so the scalar values multiplying those base functions (the "components") are not the same. So far, so good.

What I don't get now, is the following : what are the base functions such that f can be represented with the coordinates (or components) f(1), ..., f(n) ? Basically what @Mark44 said is (I think) : those are not components of any base functions / unit vectors.

I wouldn't mind that if the inner product wasn't looking the way it does. Like a dot product (sure it's an intergal, and we need to take complex conjugates if we use complex numbers, but this isn't much different). In a dot product, the scalars multiplied are vector components. Not in an inner product ? Why ?

When you're working with the inner product of a function space, the coordinates of a function aren't f(1), f(2), and so on -- the coordinates are the constants that multiply each element of a some basis for that space.

Let's say I take the inner product of functions f(t) and g(t) in two differents ways :

1 - integral of the complex conjugate of f(t) times g(t) from a to b
2 - integral of the complex conjugate of the Fourier series of f(t) time the Fourier series of g(t), from a to b

The results of those two operations are equal, right ? And both multiply two complex values inside the integral (the multiplied base functions in the Fourier series are either 1 or 0 if they are orthonormal functions).

In the case of the Fourier series, those complex values are components of the function. But not in the first case without the Fourier series ? While still both being equal operations ? That seems really odd.

 

[Stephen Tashi]

What I don't get now, is the following : what are the base functions such that f can be represented with the coordinates (or components) f(1), ..., f(n)

For example, $e_2(x)$ is the function defined by: $e_2(x) = 1$ if $x = 2$ and $e_2(x) = 0$ if $x\ne 2$.
$f(x) = ...+ f(2) e_2(x) + ...$

 

[DoobleD]

For example, e2(x)e2(x)e_2(x) is the function defined by: e2(x)=1e2(x)=1e_2(x) = 1 if x=2x=2x = 2 and e2(x)=0e2(x)=0e_2(x) = 0 if x≠2x≠2x\ne 2.
f(x)=...+f(2)e2(x)+...

Oh, of course ! That makes perfect sense. Plus this set of base functions is orthonormal, and I suppose it also spans the space since any function can be expressed as a linear combination of this set. As for example with Fourier series, a set of exponential base functions spans the space for any periodic function (hope I'm not making mistakes in those affirmations, things as still shaky for me as you can tell).

When reading your answer I thought : "this is so obvious, why didn't I see it.". Thank you very much to both of you for your time and explanations, this helped me a lot !