ViolentCorpse
- 190
- 1
This is actually a solved example of Thevenin's principle in my textbook and I understand all of it except the part that I'm attaching to this post below; the part where KVL (Kirchoff's Voltage Law) is applied.
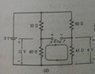
Find Eth in the circuit shown in the attached figure.
(This is not the actual question, it's just the part that I'm having problems with)
The way I've learned it, conventional current flows from + to - in resistors. But in the selected loop where Kirchoff's Voltage Law is applied, current is flowing in the 60Ω resistor from - to +. It's the polarities chosen for the resistors that is confusing me.
The way I was personally doing the problem was like this:
I started from the positive end of Eth and moved counter-clockwise in the loop, assigning the resistors their polarities according to the direction of the current that I was assuming (passing from + to - in both the resistors, by this way). By this procedure, I get:
12V + 6V = Eth
Eth = 18V
But the correct answer and the equation formed in the book is:
6V + Eth = 12V
Eth = 6V
which makes sense to me, but only after seeing the polarities assigned to the resistors. My procedure yields the same result, but only if I keep the polarities as they are shown in the figure intact. My question is, why are the polarities in the example assigned the way they are and what is wrong with the way I am doing it?
Thanks a ton guys!
P.S: If it's any help, the voltages for the two resistors were found using voltage-divider rule.
Homework Statement
Find Eth in the circuit shown in the attached figure.
(This is not the actual question, it's just the part that I'm having problems with)
The Attempt at a Solution
The way I've learned it, conventional current flows from + to - in resistors. But in the selected loop where Kirchoff's Voltage Law is applied, current is flowing in the 60Ω resistor from - to +. It's the polarities chosen for the resistors that is confusing me.
The way I was personally doing the problem was like this:
I started from the positive end of Eth and moved counter-clockwise in the loop, assigning the resistors their polarities according to the direction of the current that I was assuming (passing from + to - in both the resistors, by this way). By this procedure, I get:
12V + 6V = Eth
Eth = 18V
But the correct answer and the equation formed in the book is:
6V + Eth = 12V
Eth = 6V
which makes sense to me, but only after seeing the polarities assigned to the resistors. My procedure yields the same result, but only if I keep the polarities as they are shown in the figure intact. My question is, why are the polarities in the example assigned the way they are and what is wrong with the way I am doing it?
Thanks a ton guys!
P.S: If it's any help, the voltages for the two resistors were found using voltage-divider rule.