Karol
- 1,380
- 22
Homework Statement
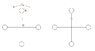
4 small balls of mass m each are connected with light rods like in the picture. the system is rotating with angular velocity ω0.
When the system is in the rightmost position the upper ball disconnects from the system.
What is the angular velocity of the 3 remaining balls
Homework Equations
Initial angular velocity round point O:
L_0=4m\omega_0 l^2
Because of preservation of linear momentum, the velocity of the C.O.M of the 3 balls is
V=\frac{\omega_0 l}{3}
The Attempt at a Solution
I am told the angular momentum is preserved, and i know the upper ball moves at
V=\omega_0 l
And the 3 remaining balls must have angular momentum of
L=3m\omega_0 l^2
And this implies they rotate at angular velocity ω0, but they rotate around their center of mass, so the directions of velocities and distances from point O change.
I know the answer is they rotate at ω0, but why?