7C0A0A5
- 10
- 0
A uniform thin rod of length 0.40 m and mass 3.5 kg can rotate in a horizontal plane about a vertical axis through its center. The rod is at rest when a 3.0-g bullet traveling in the horizontal plane of the rod is fired into one end of the rod. As viewed from above, the direction of the bullet's velocity makes an angle of 60° with the rod (Fig. 12-44).If the bullet lodges in the rod and the angular velocity of the rod is 14 rad/s immediately after the collision, what is the magnitude of the bullet's velocity just before impact? [in m/s]
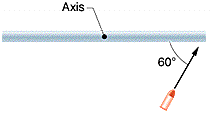
This should be a relatively easy problem, but I'm missing a concept somewhere. Please help.
First I thought that I could set Total Momentum before and after the collision equal to each other.
L = M can you do that?
L = I * \omega
M = m * V
I = {m_{final} * l^2}/12
when solving these I got 0.04671 for L
and 218 for V
but that is wrong
then I used trig to find how fast that would be at that angle and got 252
which is also wrong...can someone please tell me where I'm messing up?
This should be a relatively easy problem, but I'm missing a concept somewhere. Please help.
First I thought that I could set Total Momentum before and after the collision equal to each other.
L = M can you do that?
L = I * \omega
M = m * V
I = {m_{final} * l^2}/12
when solving these I got 0.04671 for L
and 218 for V
but that is wrong
then I used trig to find how fast that would be at that angle and got 252
which is also wrong...can someone please tell me where I'm messing up?