dodosenpai
- 8
- 0
Homework Statement
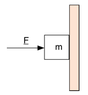
In this sketch, the mass m = 1.6 kg is pushed against a wall by force F, as shown, in the horizontal direction. The values of the coefficients of kinetic and static friction for the contact between are 0.81 and 0.84 respectively. The magnitude of F is slowly and continuously reduced. Just before the block falls, what is the total contact force Fc exerted by the block on the wall. What is the magnitude of that force and what is the angle θ it makes with horizontal? (+ve for above, -ve for below the horizontal).
Homework Equations
Ff = μsN
The Attempt at a Solution
Since the block is not moving:
Input F = N
Ff = Fg
Therefore mg = μs*N
Rearrange we get
N = mg/μs
= (1.6*9.8)/0.84
= 18.66667
= 19(2 sig. fig.)
Since Input F = N, wouldn't the contact force of the mass onto the wall be 19N? Apparently this is wrong.