Nova_Chr0n0
- 16
- 3
- Homework Statement
- The force F = 450 lb acts on the frame. Resolve this force into components acting along members AB and AC, and determine the magnitude of each component. (Figure is attached below)
- Relevant Equations
- N/A
I've already got the answer and the way to solve it (parallelogram), but I'm just wondering why I cannot use the technique I've learned in the lesson torque.
Let's focus on the line AB, if I use what I've learned in torque, the components would be like this:
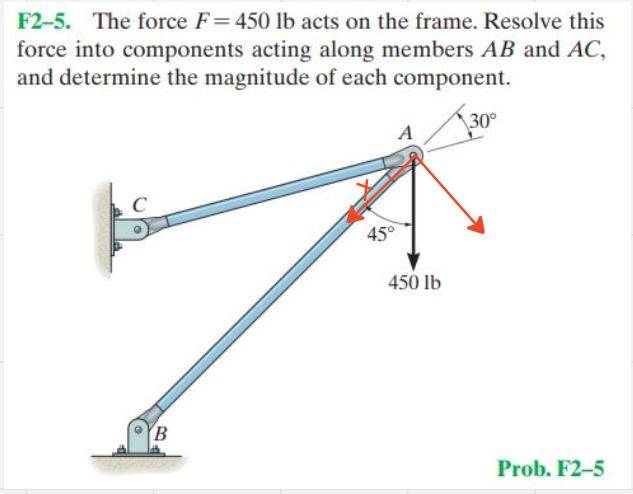
To find the force component in AB, I could just solve my assign variable "x" and use trigonometry. In this scenario I would have
x = AB = 450cos(45)
But this answer is incorrect and is not similar to when I use the parallelogram method. My question is, what is the difference between them? Is the technique only for torque/moment problems?
Let's focus on the line AB, if I use what I've learned in torque, the components would be like this:
To find the force component in AB, I could just solve my assign variable "x" and use trigonometry. In this scenario I would have
x = AB = 450cos(45)
But this answer is incorrect and is not similar to when I use the parallelogram method. My question is, what is the difference between them? Is the technique only for torque/moment problems?
