Create the free-body diagram for the scenario below.

AI Thread Summary
The discussion focuses on creating a free-body diagram for a Mercedes-Benz 300SL parked on a 15-degree incline. Participants are trying to determine the normal force and static frictional force acting on the car. There is confusion regarding the representation of gravitational force, labeled as "mg," and the correct number of forces to include in the diagram. Clarifications are requested about the vectors drawn, their directions, and the proper decomposition of gravitational force into components. The conversation emphasizes the need for accurate representation of forces to solve the problem effectively.
Clare
Messages
6
Reaction score
2

Homework Statement


A Mercedes-Benz 300SL (m = 1700 kg) is parked on a road that rises 15 degrees above the horizontal. What are the magnitudes of (a) the normal force and (b) the static frictional force that the ground exerts on the tires? Important: Assume that the road is higher up to the right and lower down to the left.
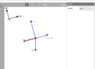
Create the free-body diagram. Please use the blue vector to specify forces.

Homework Equations


NA

The Attempt at a Solution


upload_2018-10-3_14-30-6.png

Right now I'm currently stuck with the vector highlighted in red. I just don't understand if it the angle that it is in or the length that is wrong.
 

Attachments

  • upload_2018-10-3_14-30-6.png
    upload_2018-10-3_14-30-6.png
    3.2 KB · Views: 795
Physics news on Phys.org
The diagram appears to have two forces that are labeled "mg" (one red and the other blue). What type of force does "mg" represent? How many such forces act on the car?
 
I am not able to enlarge your diagram to see things clearly. You seem to have drawn four vectors. Please list them and describe them along with statements of the direction of each.
 
I added an extra vector. I was mistakenly adding the mg sin and mg cos
 
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Thread 'Struggle to understand the concept of the question (ice cube in water optics question)'

TL;DR Summary: I came across this question from a Sri Lankan A-level textbook. Question - An ice cube with a length of 10 cm is immersed in water at 0 °C. An observer observes the ice cube from the water, and it seems to be 7.75 cm long. If the refractive index of water is 4/3, find the height of the ice cube immersed in the water. I could not understand how the apparent height of the ice cube in the water depends on the height of the ice cube immersed in the water. Does anyone have an...
View full post »

Similar threads

Center of mass and momentum- A question about systems
Replies
25
Views
1K
Forces and Free-Body Diagrams in Real-World Scenarios
Replies
5
Views
4K
Help With Drawing a Free Body Diagram
Replies
1
Views
3K
Physical interpretation of free body force diagram
Replies
13
Views
5K
Calculating Distance: Free Body Diagram for Box Sliding with Friction
Replies
1
Views
2K
Forces and Elevators: Free-Body Diagrams and Calculations
Replies
9
Views
6K
Determining the Free Body Diagram for a Dolly & Trailer
Replies
2
Views
2K
Free body diagram drawing for a two force members on machine
Replies
1
Views
5K
Help please -- Free body diagram for a weightlifter?
Replies
1
Views
7K
Free body diagram for all forces
Replies
3
Views
5K

Hot Threads

Recent Insights

Back
Top