- 3,406
- 11
The Canadian national men's curling competition (the Briar) is going on this weekend and I am motivated to write a computer program to simulate the motion of the rocks on the ice. I see on TV that the rectangular rink 14 by 126 feet appears to be trapezoidal on the screen, with the front about 7 times as wide as the far end:

I need functions to calculate the position on the trapezoid image in pixels when given the position in feet on the real rink. This strikes me as a fairly easy problem but I keep getting results that don't check out - I must have a fundamental misunderstanding. The horizontal part seems straighforward: clearly the scale of pixels per foot is larger as you move from back to front. It seems to me the vertical scale must be the same as the horizontal one at any position y down from the top or back of the trapezoidal image.
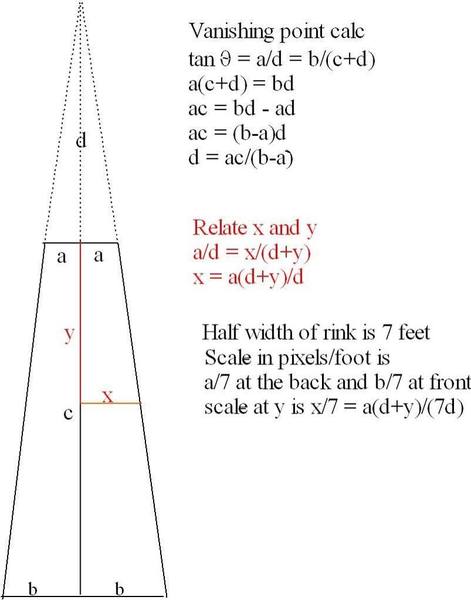
The scale I get is x pixels divided by 7 feet = a(d-y)/(7d), a linear function of the y position. My first test was to integrate the scale times dy to get the total length of the rink in feet. That came out to 126 =Bd/a[ln(d+h) - ln(d)]
I could not choose constants a,b and c to make this equal to 126 feet!
Next, I tried putting in some numbers for the a,b,c constants to make the rink image look about right on the screen and doing a spreadsheet calculation of the scale and feet for each 10 pixels of the height in the image. When I total up the feet for the whole length, I get about 50 feet.
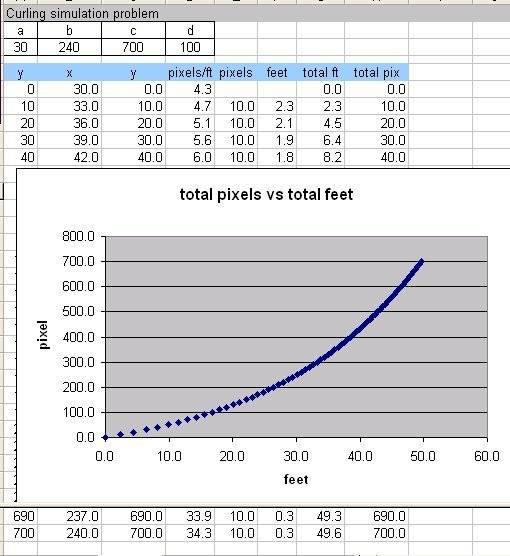
Changes to the constants for the image size and shape seem to make this total even less. Something is very wrong with my model, but what?
I need functions to calculate the position on the trapezoid image in pixels when given the position in feet on the real rink. This strikes me as a fairly easy problem but I keep getting results that don't check out - I must have a fundamental misunderstanding. The horizontal part seems straighforward: clearly the scale of pixels per foot is larger as you move from back to front. It seems to me the vertical scale must be the same as the horizontal one at any position y down from the top or back of the trapezoidal image.
The scale I get is x pixels divided by 7 feet = a(d-y)/(7d), a linear function of the y position. My first test was to integrate the scale times dy to get the total length of the rink in feet. That came out to 126 =Bd/a[ln(d+h) - ln(d)]
I could not choose constants a,b and c to make this equal to 126 feet!
Next, I tried putting in some numbers for the a,b,c constants to make the rink image look about right on the screen and doing a spreadsheet calculation of the scale and feet for each 10 pixels of the height in the image. When I total up the feet for the whole length, I get about 50 feet.
Changes to the constants for the image size and shape seem to make this total even less. Something is very wrong with my model, but what?
Last edited: