Current Calculation Problem (Probably Simple)

AI Thread Summary
The discussion centers around a basic circuit problem involving a cell with an e.m.f. of 2V and an internal resistance of 1 Ohm. The user initially struggles to calculate the current through point A and seeks assistance for clarification. After some time, the user successfully resolves the question independently. The conversation highlights the common challenges faced when learning circuit calculations. Ultimately, the user expresses relief at having solved the problem on their own.
Iscariot
Messages
7
Reaction score
0
A really basic circuit problem which I just don't understand.

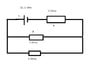
In the attached figure, C is a cell of e.m.f. 2V and internal resistance 1 Ohm. Calculate:

a) the current through A
b) the current through B
c) the p.d. between the terminals of the cell

I really don't understand how to calculate the current through A. If someone could just help me with that then I'd appreciate it, I'm hoping that from someone pointing out what's probably obvious in part A, I'll be able to do B and C by myself.
 

Attachments

  • circuit problem.jpg
    circuit problem.jpg
    7.8 KB · Views: 469
Physics news on Phys.org
Never mind, I solved my own question. Sorry about this, it took me hours.
 
Last edited:

Thread 'Struggling to understand the concept of this question (ice cube in water optics question)'

TL;DR Summary: I came across this question from a Sri Lankan A-level textbook. Question - An ice cube with a length of 10 cm is immersed in water at 0 °C. An observer observes the ice cube from the water, and it seems to be 7.75 cm long. If the refractive index of water is 4/3, find the height of the ice cube immersed in the water. I could not understand how the apparent height of the ice cube in the water depends on the height of the ice cube immersed in the water. Does anyone have an...
View full post »
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Identical Batteries in Parallel do not Draw Same Current, Non-Ideal?
Replies
7
Views
887
Current through an inductor as a function of time
Replies
10
Views
379
Current through parallel cells with unequal EMFs
Replies
2
Views
2K
Current in a circuit without external resistance
Replies
8
Views
2K
Current calculation of a Y-junction
Replies
4
Views
1K
When a short-circuit exists, how to find the current?
Replies
4
Views
2K
Why Use e.m.f. Instead of Terminal Voltage for Power Calculation?
Replies
2
Views
2K
Understanding example in Wikipedia entry for open circuit voltage
Replies
3
Views
2K
Calculating current with and without internal resistance
Replies
6
Views
3K
How does an eddy current brake work exactly?
Replies
2
Views
2K

Hot Threads

Recent Insights

Back
Top