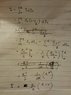Aviegaille
- 7
- 0
Homework Statement
(a)The current density across a cylindrical region of radius R varies according to the equation: J=J0(1-r/R), where r is the distance from the axis of the cylinder. The current density is the maximum J0 at the axis r=0 and decreases linearly to zero at the surface r=R. Calculate the current in terms J0 and the region's cross sectional area A=pi*R^2.
(b) Now suppose that a current density was a maximum Jo at the surface and decreased linearly to zero at the axis, so that: J=J0 r/R. Calculate the current. Why is the result different for these two cases?
Homework Equations
I=JA
The Attempt at a Solution
I uploaded a picture of the first part but I am not sure if it's correct. I also don't know how to get the area from this problem. I am thinking of plugging the value of R from I to get the area but I am pretty sure it is not right.