- #1
RoyalFlush100
- 56
- 2
Homework Statement
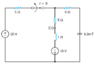
"The switch in the circuit in the figure has been closed for a long time and is opened at t = 0. Find i(50 ms)."
I attached an image of the circuit below.
Homework Equations
KVL:
Ri + q(t)/C - q(0)/C + vc(t) + Li' = vs(t)
Li'' + Ri' + i/C = vs'(t)
Where vc is voltage across the capacitor and vs is the source voltage. Q is the charge flowing through the current.
The Attempt at a Solution
First I found i(t) through the inductor and the vc prior to the switch opening:
30 = 10i --> i = 3 A
20-vc = 5i --> vc = 5 V
Now, I applied the second equation and this is where I become confused. It has to do with the application of Kirchhoff's Voltage Law. i goes through the bottom of the capacitor, so I don't know how to set up the equation.
Li'' + Ri' + i/C = 0
i'' + 10i' + 25i = 0 This?
i'' + 10i' - 25i = 0 Or this?
Likewise, I'll need to find i'(0) after. Would that be:
Ri + q(t)/C - q(0)/C + vc(t) + Li' = vs(t)
10 + 5 + i' = 10 This?
10 - 5 + i' = 10 Or this?
I think it should be minus in both cases, but the numbers behave weirdly when I try that.