stunt022
- 2
- 0
hey this is my first post, need help with a homework problem.
What is the cyclotron frequency in a 3.55 T magnetic field of the ions listed below? The masses of the atoms are shown in the table. The accuracy of your answers should reflect the accuracy of the data given below. (Although N2+ and CO+ both have a nominal molecular mass of 28, they are easily distinguished by virtue of their different cyclotron resonance frequencies.)
Atomic masses
12C 12.0000 u
14N 14.0031 u
16O 15.9949 u
(a) N2+ in MHz?
(b) O2+ in MHz?
(c) CO+ in MHz?
(numbers are subscript)
i used the following formula to try and get the answer
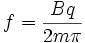
so i plugged in the numbers and got an equation that looked like this:
f = [[(3.55)*(1.6022*10^-19)]/[2*pi*((2*14.0031)*(1.66053886*10^-27))]]*10^-6
which gave me 1.946533MHz, and is wrong...
i used a charge of a proton(1.6022*10^-19) for q, for m i multiplied the atomic mass by 2 because there are 2 of them, and converted the amu into kilograms after that. finally i converted to MHz from Hz.
the only thing that might not seem right to me is the charge because of how the problem is described but i don't know what that would be.
for (b) O2+ i got 1.704137 MHz
for (c) CO+ i got 1.9473 MHz
which were wrong too.
any help on this i would appreciate.
What is the cyclotron frequency in a 3.55 T magnetic field of the ions listed below? The masses of the atoms are shown in the table. The accuracy of your answers should reflect the accuracy of the data given below. (Although N2+ and CO+ both have a nominal molecular mass of 28, they are easily distinguished by virtue of their different cyclotron resonance frequencies.)
Atomic masses
12C 12.0000 u
14N 14.0031 u
16O 15.9949 u
(a) N2+ in MHz?
(b) O2+ in MHz?
(c) CO+ in MHz?
(numbers are subscript)
i used the following formula to try and get the answer
so i plugged in the numbers and got an equation that looked like this:
f = [[(3.55)*(1.6022*10^-19)]/[2*pi*((2*14.0031)*(1.66053886*10^-27))]]*10^-6
which gave me 1.946533MHz, and is wrong...
i used a charge of a proton(1.6022*10^-19) for q, for m i multiplied the atomic mass by 2 because there are 2 of them, and converted the amu into kilograms after that. finally i converted to MHz from Hz.
the only thing that might not seem right to me is the charge because of how the problem is described but i don't know what that would be.
for (b) O2+ i got 1.704137 MHz
for (c) CO+ i got 1.9473 MHz
which were wrong too.
any help on this i would appreciate.