jsrev
- 4
- 0
Homework Statement
A cylinder of mass M and radius R, with moment of inertia:
I_c = \frac{1}{2}MR^2
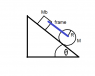
rolls down without slipping through an inclined plane with an angle of θ, while pulling a block of mass Mb with an attached frame (of insignificant mass) which is connected to the axis of the cylinder.
If the cylinder rolls without slipping over the surface and the coefficient of kinetic friction between the block Mb and the surface is μ, then:
a. Deduct an expression for the linear acceleration of the system.
This problem didn't come with a figure, but I made one based on what I think the system looks like.
See figure http://imgur.com/HyiUSLu
Homework Equations
Linear acceleration
The Attempt at a Solution
I've tried a few ways, like calculating the linear acceleration of each object (the cylinder and the block) but there are some things I don't get.
I have tried calculating
a_{cylinder} = \frac{gsinθ}{k}
given that k is a constant that equal 1/2 from the first equation. Then I got the linear acceleration of the block with a_{block} = gsinθ and also considered the friction, but I'm not any close to the answer.
The given solution is:
a = \frac{2g[(M+M_b)sinθ-μM_bcosθ]}{3M + 2M_b}
If anyone can guide me a little bit in this one I would really appreciate it. Thank you.