peter010
- 31
- 0
Hiz
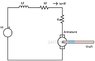
lets assum we have a load fixed on the roter of a the 'DC series motor' in the attached photo, where:
Vt: DC source voltage (constant)
Lf: field's inductive resistance (will be neglected)
Rf: field's resistant
Ra: Armature resistance
Ia= Armature current, If: field current
M: back emf (Ea)
and the related functionl equation is:
kQw (Ea)= (Vt-Ia(Ra+Rs)/kQ ; //Q:flux
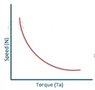
Now, if the load is doubled, then by applying kerckhoff laws, the armature current must be reduced. Anyhow, this seems to me contradicts with this motor characteristic of which that current increases as torque or load increases (kindly find the second attached photo), in other words: Torque = KQI.
Its really confusing! I spent one day trying to sort it out uselessly.
Appreciate your help to understant this.
lets assum we have a load fixed on the roter of a the 'DC series motor' in the attached photo, where:
Vt: DC source voltage (constant)
Lf: field's inductive resistance (will be neglected)
Rf: field's resistant
Ra: Armature resistance
Ia= Armature current, If: field current
M: back emf (Ea)
and the related functionl equation is:
kQw (Ea)= (Vt-Ia(Ra+Rs)/kQ ; //Q:flux
Now, if the load is doubled, then by applying kerckhoff laws, the armature current must be reduced. Anyhow, this seems to me contradicts with this motor characteristic of which that current increases as torque or load increases (kindly find the second attached photo), in other words: Torque = KQI.
Its really confusing! I spent one day trying to sort it out uselessly.
Appreciate your help to understant this.
 )))))
)))))