De broglies wavlength and energy

[SpartanG345]

I am having a little trouble understanding de Broglies equation and wavelength and it relation ship with energy

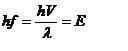
by E=hf and debroglies equation the above equation will get the energy of the particle
i did an example and i found this energy does not = the Kinetic energy of the particle, infact it was smaller

why is this

I thought E = hf only applies to zero mass particles?

 

[Delphi51]

My understanding is from high school physics (I finished my physics degree 30 some years ago). De Broglie's insight, found while drinking beer in a pub, was that perhaps waves have momentum p = h/λ and particles have wavelength λ = h/p. I don't think E=hf applies to anything other than photons.

 

[kerimek]

De Broglie's equation and wavelength are important concepts in quantum mechanics that help us understand the behavior of particles at the atomic and subatomic level. The equation, λ = h/mv, relates the wavelength (λ) of a particle to its momentum (mv) and Planck's constant (h). This suggests that all particles, regardless of their mass, have a wave-like nature and exhibit wave-like properties such as wavelength.

The equation E = hf, known as the Planck-Einstein relation, relates the energy (E) of a particle to its frequency (f) and Planck's constant (h). This equation applies to all particles, including those with mass. However, it is important to note that this equation gives the total energy of a particle, including its rest energy and its kinetic energy.

In your example, you found that the energy calculated using E = hf was smaller than the kinetic energy of the particle. This is because the equation takes into account the rest energy of the particle, which is a constant value and cannot be changed. The kinetic energy, on the other hand, can vary depending on the velocity of the particle.

It is important to understand that de Broglie's equation and the Planck-Einstein relation are not contradictory. They simply describe different aspects of a particle's behavior. De Broglie's equation helps us understand the wave-like nature of particles, while the Planck-Einstein relation helps us calculate their total energy.

I hope this helps clarify the relationship between de Broglie's wavelength and energy. If you have any further questions, please let me know.