jkthejetplane
- 29
- 4
- Homework Statement
- Using the Debye approximation, illustrate how the phonon heat capacity changes with
respect to temperature in 1D. Discuss your results in the low and high temperature limit
respectively.
- Relevant Equations
- equations of Cv from book in 3d listed below
So really i am just unsure how to answer the last part of the question. I am unsure how to apply the low and high temperature limits the way i have done it. Do i set upper/lower limits on the integral and solve? If so i am not sure what to put
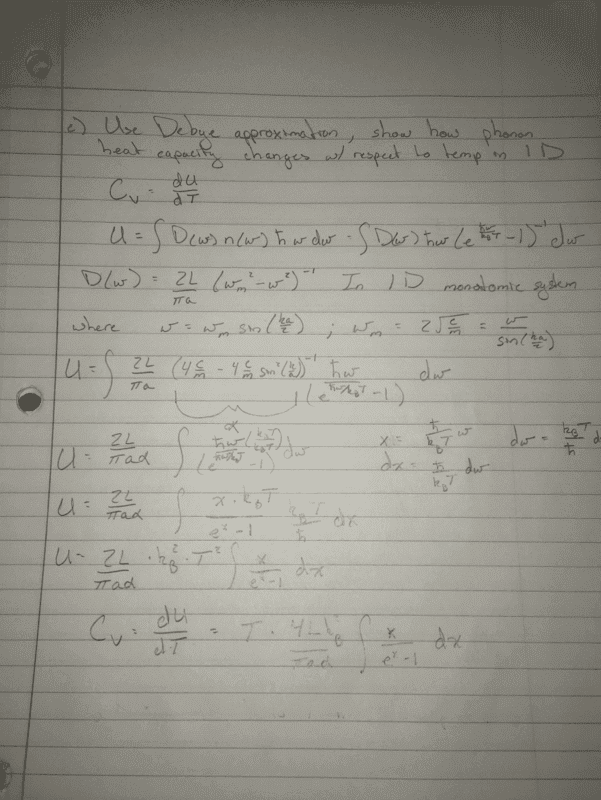
Here is what he book has for 3d
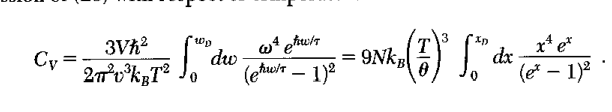
Here is what he book has for 3d