- #1
Rumplestiltskin
- 97
- 3
Not a homework problem, so not sure if this is in the right area. Thought it was too sophomore to post in the maths forums.
So, when you integrate y within defined limits for x, you get the area between the graph and the x-axis within those limits for x. But
a) Why is this always between the graph and the x-axis, as if you've also defined limits for y (y=0 to y=maximum or minimum point)? Your answer would be infinite if you didn't define limits for y, so it's in there somewhere.
b) Wouldn't integration give you the area above and below the x-axis, within the defined limits? So in the below example, it would give you the area x + y. We had a problem in class where this parabola was transformed a little up, and when integrated only found the larger area x. Does integration only give you the larger area bounded by a graph and the x-axis?
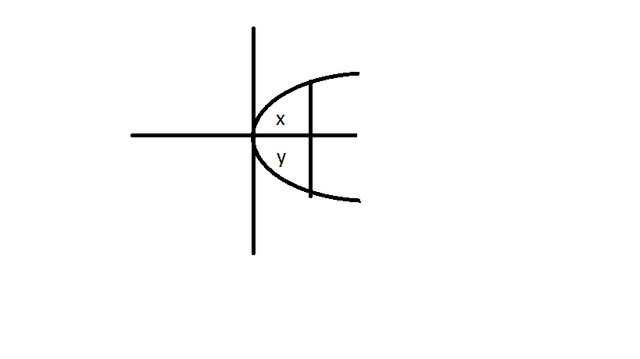
So, when you integrate y within defined limits for x, you get the area between the graph and the x-axis within those limits for x. But
a) Why is this always between the graph and the x-axis, as if you've also defined limits for y (y=0 to y=maximum or minimum point)? Your answer would be infinite if you didn't define limits for y, so it's in there somewhere.
b) Wouldn't integration give you the area above and below the x-axis, within the defined limits? So in the below example, it would give you the area x + y. We had a problem in class where this parabola was transformed a little up, and when integrated only found the larger area x. Does integration only give you the larger area bounded by a graph and the x-axis?