CMBR
- 13
- 0
Homework Statement
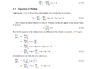
So this isn't a homework problem but I don't know where else I am supposed to post for general help. I am basically trying to understand the derivation for the equation of motion of a particle in a rotating frame. See attachment for derivation and which steps I am stuck on.
Homework Equations
The Attempt at a Solution
From where the yellow dots are marked is where I get confused, since v_I=v_R+w\times r
why does: \dot{v}_I|_{I} = \dot{v}_R|_{I} + w\times v_I Theres 2 reasons this step is confusing me, if I am taking a time derivative of v_I=v_R+w\times r shouldn't I be using the product rule on the 2nd term in the RHS \dot{v}_I|_{I} = \dot{v}_R|_{I} + \frac{\mathrm{d} }{\mathrm{d} t}[w\times r]|_{I} ?
Secondly if that's just wrong the derivation does say to use (1.2.5) but then the 1st term on the RHS should be \dot{v}_I|_{R} instead of \dot{v}_R|_{I} no? But if that is the case then I don't see how to get to the step after that either... Really could use some help, thanks in advance.
[EDIT: I should specify that the I and R means inertial and rotational respectively]