Derivation of time period for physical pendula without calculus

[danpendr]

TL;DR Summary: I'm stuck trying to find the equation for time period T of a physical pendulum without any calculus using torque.

Hello all.

I am currently writing my IB Physics HL IA (high school physics lab report).

I am investigating the effect of length on the time period of a uniform rod pendulum.

I need to derive the following equation, ideally without using calculus:

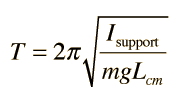
This website has a good derivation but skips an important step at the end, when stating "This is identical in form to the equation for the simple pendulum and yields a period: EQUATION ABOVE". I was wondering if there was a way to arrive to the equation without jumping through hoops. If anyone could help me continue my derivation I'd be very appreciative. I got as far as this:

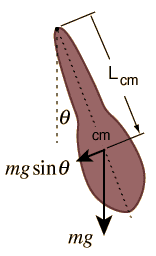
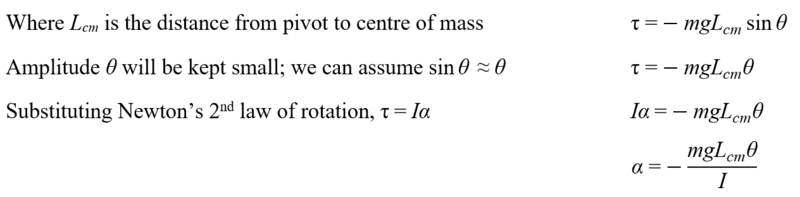
Kind regards
Dan

 

[haruspex]

Consider a point on the periphery of a disc rotating at constant speed. What is the relationship between the disc's rotation angle at some instant, the x coordinate of the point and the component of its acceleration in the x direction?

 

[danpendr]

Consider a point on the periphery of a disc rotating at constant speed. What is the relationship between the disc's rotation angle at some instant, the x coordinate of the point and the component of its acceleration in the x direction?

haruspex, thank you for your response, but I don't seem to understand. What do you mean by x-coordinate?

Could you show your working out?

Many thanks
Dan

 

[haruspex]

What do you mean by x-coordinate?

Take a disc radius r to be rotating about the origin in the XY plane at angular velocity ω. For a point on the perimeter, what is the relationship between its x coordinate and the x component of its acceleration?