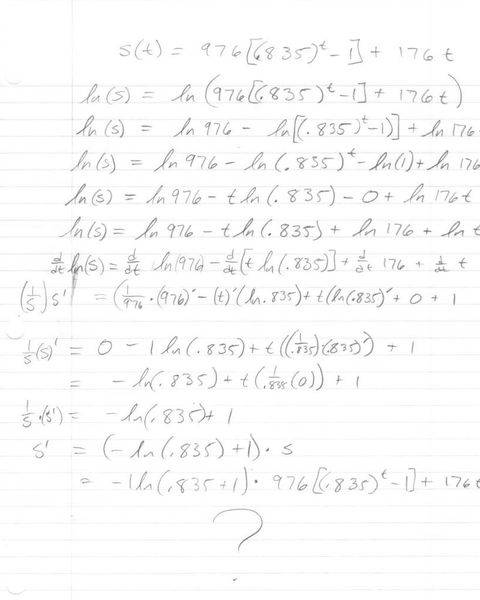Derivative of s(t) = (976(.835)^t -1) + 176t using log differentiation

[LearninDaMath]

1. Homework Statement

The derivative of s(t) = (976(.835)^t - 1) +176t

I have to take ln of both sides to bring the t down from the exponent. But I never had to apply ln to an equation of this complexity. Here is my attempt, but it doesn't even look close to being on the correct path...what I'm I doing wrong? I'm guessing I'm messing up a step pretty early on in this problem. Can you locate my confusion? EDIT: the t on the 176t got cut off when scanned, but its supposed to be there on the 3rd and 4th lines..

 

[Office_Shredder]

ln does not do what you want it to do. Once you take ln you're basically done as far as simplifying the equation is concerned. Of course, at that point you could just use the chain rule, but that requires differentiating the original equation as well, which begs the question: why are you taking ln before differentiating if all you want is the derivative of s(t)?

 

[SammyS]

Homework Statement

The derivative of s(t) = (976(.835)^t - 1) +176t

I have to take ln of both sides to bring the t down from the exponent. But I never had to apply ln to an equation of this complexity. Here is my attempt, but it doesn't even look close to being on the correct path...what I'm I doing wrong? I'm guessing I'm messing up a step pretty early on in this problem. Can you locate my confusion?

EDIT: the t on the 176t got cut off when scanned, but its supposed to be there on the 3rd and 4th lines..

Isolate (on one side of the equation) the 976(.835)^t, or (.835)^t before taking the logarithm.

 

[LearninDaMath]

ln does not do what you want it to do. Once you take ln you're basically done as far as simplifying the equation is concerned. Of course, at that point you could just use the chain rule, but that requires differentiating the original equation as well, which begs the question: why are you taking ln before differentiating if all you want is the derivative of s(t)?

This is the general idea of whre I'm trying to go with this question:

...And I'm trying to fill in the steps that might have been skipped here. All i know about using logs is that when there are variables in the exponent you can take ln of both sides to simplify before differentiating. But I'm not sure if I'm understanding how or when, within this particular problem, to take the ln of both sides.

 

[LearninDaMath]

Isolate (on one side of the equation) the 976(.835)^t, or (.835)^t before taking the logarithm.

not exactly sure what u mean. Do u mean that when taking ln of both sides of an equation, all terms should be distributed (so that there are no parenthesis)?

For instance, if I have S = A(B^{t} + C)

And I want to take ln of both sides, I must first do this:

S = AB^{t} +AC

and only then I can take ln:

lnS = ln(AB^{t} + lnAC)

which becomes

LnS = lnAB^{t} + lnAC

would be what you're saying?

 

[Office_Shredder]

The key here isn't to use natural logs, it's to use properties of derivatives. Let me do a simpler example and you can try expanding it to this problem. Calculate the derivative of
s(t) = 3*(.5^t)+t

\frac{d}{dt} \left( 3*(.5^t)+t \right) = \frac{d}{dt} \left(3*.5^t \right) + \frac{d}{dt} \left( t \right)
= 3 \frac{d}{dt}(.5^t) + \frac{dt}{dt}
the derivative of t as a function of t is just t. To differentiate .5^t we use the exponential rule d/dt(a^t) = \ln(a) a^t to get
= 3*\ln(.5) .5^t+1

 

[SammyS]

Isolate (on one side of the equation) the 976(.835)^t, or (.835)^t before taking the logarithm.

Another way to say this is:

Solve your equation for 976(.835)^t, or (.835)^t, before taking the log of both sides.​

not exactly sure what u mean. Do u mean that when taking ln of both sides of an equation, all terms should be distributed (so that there are no parenthesis)?

 

[LearninDaMath]

The key here isn't to use natural logs, it's to use properties of derivatives. Let me do a simpler example and you can try expanding it to this problem. Calculate the derivative of
s(t) = 3*(.5^t)+t

\frac{d}{dt} \left( 3*(.5^t)+t \right) = \frac{d}{dt} \left(3*.5^t \right) + \frac{d}{dt} \left( t \right)
= 3 \frac{d}{dt}(.5^t) + \frac{dt}{dt}
the derivative of t as a function of t is just t. To differentiate .5^t we use the exponential rule d/dt(a^t) = \ln(a) a^t to get
= 3*\ln(.5) .5^t+1

So if I have s = .5^{t}

if I go right into differentiating, i'll get

ds/dt = t(.5)^{t-1}(0) so that

ds/dt = 0

However, if I use the exponenent rule, i'll get

ds/dt = d/dt ln(.5^{t}) = ln(.5)*(.5^{t})

Would that be correct?

 

[SammyS]

So if I have s = .5^{t}

if I go right into differentiating, i'll get

ds/dt = t(.5)^{t-1}(0) so that

ds/dt = 0

However, if I use the exponenent rule, i'll get

ds/dt = d/dt ln(.5^{t}) = ln(.5)*(.5^{t})

Would that be correct?

The point of doing logarithmic differentiation is;

If s = (0.5)^t ,

then ln(s) = t ln(0.5) .​

Differentiating that should be easy.

 

[Office_Shredder]

So if I have s = .5^{t}

if I go right into differentiating, i'll get

ds/dt = t(.5)^{t-1}(0) so that

You cannot use the power rule on something of the form a^t

 

[LearninDaMath]

You cannot use the power rule on something of the form a^t

Okay, then I'm confused at the moment. If you can't use the power rule on a^{t}, then how does a^{t} differ from (.5^{t})?

I'm asking because it seems to differ from the state rule:

To differentiate .5^t we use the exponential rule d/dt(a^t) = \ln(a) a^t

EDIT: Wait, Wait...by power rule, are referring to chain rule? If so, then I do understand that power/chain rule can't be applied to a^t because there is a variable as the exponent, right? However, if you are saying that the exponential rule can't be applied to a^t, then I am definitely confused.

 

[LearninDaMath]

Homework Statement

The key here isn't to use natural logs, it's to use properties of derivatives. Let me do a simpler example and you can try expanding it to this problem. Calculate the derivative of
s(t) = 3*(.5^t)+t

\frac{d}{dt} \left( 3*(.5^t)+t \right) = \frac{d}{dt} \left(3*.5^t \right) + \frac{d}{dt} \left( t \right)
= 3 \frac{d}{dt}(.5^t) + \frac{dt}{dt}
the derivative of t as a function of t is just t. To differentiate .5^t we use the exponential rule d/dt(a^t) = \ln(a) a^t to get
= 3*\ln(.5) .5^t+1

------------------------------------------
So if I have s = .5^{t}

if I go right into differentiating, i'll get

ds/dt = t(.5)^{t-1}(0) so that

ds/dt = 0 , which is incorrect as we both agree.
-------------------------------------------------------

ln(s) = ln(.5^{t}) so that

ln(s) = t(ln(.5)) , then finally differentiating,

d/dt lns = d/dt (t(ln(.5))

d/dt lns = t'(ln(.5)) + t(ln(.5))'

d/dt lns = ln(.5) + t(1/5)(.5)'

d/dt lns = ln(.5)

(1/s)(s)' = ln(.5)

(s)' = ln(.5)(s)

(s)' = ln(.5)*(.5^{t})

Which can get messy and increase likelyhood of mistakes.

------------------------------------------------------------However, if I use the exponenent rule, i'll get

ds/dt = d/dt ln(.5^{t}) = ln(.5)*(.5^{t})

Which is the same answer, but much more effiecient.
------------------------------------------------------------So can it be said that when there's a constant to the power of the variable, you can't just do chain rule, or else you'll get an incorrect answer. You can technically take ln of both sides and then differentiate, but it will be messy and complicated. So the best approach would be to apply the exponental rule.

If that is correct, then my confusion now is how i would apply the exponential rule to various functions. For instance, in the original function: s(t) = (976(.835)^t - 1) +176t

Would I apply derivative rules as usual, except when I get to (.835^t), instead of using the chain rule, i use the exponent rule. Then, the 976 gets moved to the side by the constant multiple rule, the d/dx gets applied to .835^t and -1 and 176t. All the rules apply except instead of the chain rule on .835^t, the exponent rule is applied, therefore employing the use of the ln within that one term. The contant of (-1) disappears, the 176t becomes 176 and thus, the equation has been derived by using the exponent rule.

I think I understand it now, thanks! I feel like I've made tremendous progress here in understanding this new rule of differentiation. I think I've seen the property before, but i guess it faded away since I never actually had to apply it to a problem until today. Thanks.

EDIT: Well, i at least think I have it correct and fully understood. Could you let me know if I said it correctly in t

 

[LearninDaMath]

The point of doing logarithmic differentiation is;

If s = (0.5)^t ,

then ln(s) = t ln(0.5) .​

Differentiating that should be easy.

Easy and produces the same correct answer, but requiring more work than using the exponential rule as shredder mentions. Would you agree?

 

[Office_Shredder]

The power rule is \frac{d}{dt} t^n = nt^{n-1} A common mistake, which you appeared to try, is to do it when the variable is in the exponent: \frac{d}{dt} a^t = t a^{t-1} which is not true

 

[LearninDaMath]

The power rule is \frac{d}{dt} t^n = nt^{n-1} A common mistake, which you appeared to try, is to do it when the variable is in the exponent: \frac{d}{dt} a^t = t a^{t-1} which is not true

Oh, that's the power rule...i just thought of it as the chain rule, but I do see the distinction. It's the chain rule, but doesn't go through the extra steps of taking the derivative of the inside term since it is automatically known that the inside term will be 1. However in this case, the derivative of the inside term will be zero, which is incorrect. I understood it, just mixed up the name for it. I used the power rule just to make the distinction between it and the exponential rule..I should have made note of that as I did in the post after that one.

P.S. I've been trying to use the "edit post" option to go back and copy & paste some of the equations i'd be using multiple times within this thread so as to avoid having to rewrite the equations over and over (still getting the hang of the latex language) and with all the copying and pasting I accidently edited the post # 1 with what I was trying to post as post #12. Luckily, I was able to piece it back together as it originally was, so there was a 2 minute span that might have been confusing if you were trying to read the first post. Anyway, thanks Shredder and Sammy for your help.

 

[SammyS]

Easy and produces the same correct answer, but requiring more work than using the exponential rule as shredder mentions. Would you agree?

Which way is more work?

It's a matter of personal preference.

Since the thread title had "log differentiation" in it, I pushed in that direction.

According to post #4, it looks like the initial problem is to differentiate the function s(t) = 976{(.835)^t - 1} +176t .

After a bit of algebra:

\displaystyle s(t)-176t+976=976(0.835)^t​

Taking the natural log of this gives

\displaystyle \ln\left(s(t)-176t+976\right)=\ln\left(976(0.835)^t\right)

\displaystyle =\ln(976)+t\ln(0.835)​

Differentiating this gives

\displaystyle \frac{s'(t)-176}{s(t)-176t+976}=\ln(0.835)

Finally,

\displaystyle s'(t) = 176 + \left(s(t)-176t+976\right)\ln(0.835)

\displaystyle = 176 + \left(976\left((.835)^t- 1\right) +176t-176t+976\right)\ln(0.835)

\displaystyle = 176 + \left(976(.835)^t \right)\ln(0.835)
​

 

[LearninDaMath]

It really is awesome to live in an age where information flows so freely ..and I'm appreciative of being able to see this problem from various perspectives. Thanks SammyS. I look at this equation now and it's not nearly as daunting as it seemed yesterday.

 

[LearninDaMath]

post #2:

ln does not do what you want it to do. Once you take ln you're basically done as far as simplifying the equation is concerned. Of course, at that point you could just use the chain rule, but that requires differentiating the original equation as well, which begs the question: why are you taking ln before differentiating if all you want is the derivative of s(t)?

How could I use chain rule at that point if there is no composition of functions?

 

[Ray Vickson]

1. Homework Statement

The derivative of s(t) = (976(.835)^t - 1) +176t

I have to take ln of both sides to bring the t down from the exponent. But I never had to apply ln to an equation of this complexity. Here is my attempt, but it doesn't even look close to being on the correct path...what I'm I doing wrong? I'm guessing I'm messing up a step pretty early on in this problem. Can you locate my confusion?


EDIT: the t on the 176t got cut off when scanned, but its supposed to be there on the 3rd and 4th lines..

You made an error going from line 4 to line 5: ln[ .835^t - 1] is NOT ln(.835^t) - ln(1).
For example, log(5-1) is not log(5) - log(1) = log(5), because 5-1 is not 5. Anyway, I honestly cannot see why you bother taking logs. If I were doing the question I would write 0.835 = e^c (c = ln(0.835), and go on from there.

RGV

 

[LearninDaMath]

Isolate (on one side of the equation) the 976(.835)^t, or (.835)^t before taking the logarithm.

Which way is more work?

It's a matter of personal preference.

Since the thread title had "log differentiation" in it, I pushed in that direction.

According to post #4, it looks like the initial problem is to differentiate the function s(t) = 976{(.835)^t - 1} +176t .

After a bit of algebra:

\displaystyle s(t)-176t+976=976(0.835)^t​

Taking the natural log of this gives

\displaystyle \ln\left(s(t)-176t+976\right)=\ln\left(976(0.835)^t\right)

\displaystyle =\ln(976)+t\ln(0.835)​

Differentiating this gives

\displaystyle \frac{s'(t)-176}{s(t)-176t+976}=\ln(0.835)

Finally,

\displaystyle s'(t) = 176 + \left(s(t)-176t+976\right)\ln(0.835)

\displaystyle = 176 + \left(976\left((.835)^t- 1\right) +176t-176t+976\right)\ln(0.835)

\displaystyle = 176 + \left(976(.835)^t \right)\ln(0.835)
​

Sammy, what would be the logic or rationale for deciding to isolate 976(.835)^t, or (.835)^t before taking the logarithm? ..as opposed to just taking the logarithm as it is with s(t) isolated?

 

[LearninDaMath]

You made an error going from line 4 to line 5: ln[ .835^t - 1] is NOT ln(.835^t) - ln(1).
For example, log(5-1) is not log(5) - log(1) = log(5), because 5-1 is not 5. Anyway, I honestly cannot see why you bother taking logs. If I were doing the question I would write 0.835 = e^c (c = ln(0.835), and go on from there.

RGV

If I have:

ln[.835^t - 1] = ln[.835^t - 1]

so we can say: ln[5-1] = ln[5-1]

ln5 - ln1 = ln[5-1]

ln5 - ln1 = ln4

This is not correct?

 

[LearninDaMath]

Btw Ray, my last post was in regard to this portion of your response:

You made an error going from line 4 to line 5: ln[ .835^t - 1] is NOT ln(.835^t) - ln(1).
For example, log(5-1) is not log(5) - log(1) = log(5), because 5-1 is not 5.

I think I understand.. ln5 - ln1 = ln5 - 0 = 5 , so ln[5-1] = ln4 and ln5≠ln4, thus ln[5-1] ≠ ln5 - ln1. Is this correct? If so, then what would be the proper way of applying ln to a function with ln[ .835^t - 1]? Note that although this method differs from the ones being discussed in this thread currently (using derivatives instead of taking log of both sides), i'd also like to see this perspective as well.

And, I'm also interested to know what you mean by writing .835 = e^c and going from there. Would you raise the entire right side of the equation by e or just ln(.835):

Anyway, I honestly cannot see why you bother taking logs. If I were doing the question I would write 0.835 = e^c (c = ln(0.835), and go on from there.

RGV

 

[LearninDaMath]

Okay, as of now, I completely understand how to find the derivative of this function. I can find it three different ways: One method, taking derivative first (implementing exponential rule) w/o taking ln of both sides. Another method, isolating 976(.835)^t, then taking ln of both sides. And lastly, taking ln of both sides from the start. And I would not have been able to figure out a single method without help from PF. Appreciate the help. And it turns out, the final missing piece of the knowledge puzzle was the fact that I didn't know that ln(a+b)≠ln(a)+ln(b). Again, thanks for all the help on this problem.

One final question. Ray Vickson, you state that:

"If I were doing the question I would write 0.835 = e^c (c = ln(0.835), and go on from there."

Could you elaborate on that? I'm not following.

 

[Ray Vickson]

If I have:

ln[.835^t - 1] = ln[.835^t - 1]

so we can say: ln[5-1] = ln[5-1]

ln5 - ln1 = ln[5-1]

ln5 - ln1 = ln4

This is not correct?

Of course not! Why on Earth would you ever even ask? You have ln 1 = 0, so you *cannot* have ln 5 - ln 1 = ln 4---that would say that ln 5 = ln 4, or 5 = 4.

RGV

 

[SammyS]

Sammy, what would be the logic or rationale for deciding to isolate 976(.835)^t, or (.835)^t before taking the logarithm? ..as opposed to just taking the logarithm as it is with s(t) isolated?

The reason that I suggested isolating 976(.835)^t was that the title of this thread indicated that you were to find s'(x) "using log differentiation".

Taking the log of a sum or difference doesn't lend itself to any simplification.

Taking the log of a quantity the has the variable in the exponent can be very helpful. It allows the variable to be moved from the exponent to the main line of the expression.

If you don't have to use log differentiation, then (provided you know how to differentiate e^x and use the chain rule) I would suggest using the following, as suggested by Ray Vickson:

\displaystyle A=e^{\,\ln{(A)}}

So that, \displaystyle 0.835^t=\Large{e^{\ln{\left(0.835^t\right)}}}= \large e^{(t)\ln{\left(0.835\right)}}

It's easy to differentiate that.​

 

[Ray Vickson]

Btw Ray, my last post was in regard to this portion of your response:



I think I understand.. ln5 - ln1 = ln5 - 0 = 5 , so ln[5-1] = ln4 and ln5≠ln4, thus ln[5-1] ≠ ln5 - ln1. Is this correct? If so, then what would be the proper way of applying ln to a function with ln[ .835^t - 1]? Note that although this method differs from the ones being discussed in this thread currently (using derivatives instead of taking log of both sides), i'd also like to see this perspective as well.

And, I'm also interested to know what you mean by writing .835 = e^c and going from there. Would you raise the entire right side of the equation by e or just ln(.835):

0.835 = e^c, so (0.835)^t = (e^c)^t = e^(ct). Differentiating e^(ct) is easy.

PS: My previous response (posted just a minute ago) was done before seeing this latest one. I want to delete it but cannot find a 'delete' button.

RGV

 

[LearninDaMath]

Of course not! Why on Earth would you ever even ask? You have ln 1 = 0, so you *cannot* have ln 5 - ln 1 = ln 4---that would say that ln 5 = ln 4, or 5 = 4.

RGV

LOL, of course this is incorrect. However, I didn't know it at the time of posting though lol. It was only after the fact, when your first response lead me to check up on the various log rules did i realize this. And to think, this log property happened to be the cause of most of my confusion from the very start of this thread. It was the reason I kept trying to distribute ln into the left side of the equation.

The silver lining though, because of asking for clarification on this function, is that I now understand how to take the derivative in various ways and I feel that much more confident about using the various rules of deriving functions.

0.835 = e^c, so (0.835)^t = (e^c)^t = e^(ct). Differentiating e^(ct) is easy.

PS: My previous response (posted just a minute ago) was done before seeing this latest one. I want to delete it but cannot find a 'delete' button.

RGV

Eh, no prob, at least you haven't posted a calculus question in the physics section (and visa versa) like I've done...that would have been a good use for a delete button. No worries. Thanks for explaining .835 = e^c further.

 

[LearninDaMath]

Confusion once more. I'm studying up on some logarithms and am a little perplexed by this problem that seems to conflict with the log property log(5 - 1) ≠ log(5) - log(4)

Line 3 to 4, log3 is being distributed into a parenthesis of (x-2) and log4 is distributed into (2x+1).

Can this occur because (x-2) and (2x+1) are not the number actually connected to the log (such as 3 in log3 and 4 in log4)?

 

[LearninDaMath]

The reason that I suggested isolating 976(.835)^t was that the title of this thread indicated that you were to find s'(x) "using log differentiation".

Taking the log of a sum or difference doesn't lend itself to any simplification.

Taking the log of a quantity the has the variable in the exponent can be very helpful. It allows the variable to be moved from the exponent to the main line of the expression.

If you don't have to use log differentiation, then (provided you know how to differentiate e^x and use the chain rule) I would suggest using the following, as suggested by Ray Vickson:

\displaystyle A=e^{\,\ln{(A)}}

So that, \displaystyle 0.835^t=\Large{e^{\ln{\left(0.835^t\right)}}}= \large e^{(t)\ln{\left(0.835\right)}}

It's easy to differentiate that.​

Thanks Sammy,

I'm trying right now to look up that property of e to the power of lnx that you and Ray have shown to be another method.

 

[SammyS]

What is log_b(A) ?

log_b(A) is the exponent that you use with a base of b to get A as a result.

 

[LearninDaMath]

What is log_b(A) ?

log_b(A) is the exponent that you use with a base of b to get A as a result.

Okay, that is kind of a tricky concept but I get it the idea of the property. I get the fact that A = e^ln(A). However in regard to the function:

s(t) = 976[.835^t - 1] + 176t

I'm trying to figure out how to apply it. The way I'm understanding this property is that it is used when trying to eliminate a log from an equation.

And so I'm not exactly sure how it can be applied to find the derivative.

If I have fx = b^x,

and I take ln of both sides: lnfx = ln(b^x)

Should I apply the property at this point to both sides: e^(lnfx) = e^ln(b^x)

Then I get e^(lnfx) = e^xlnb

And then, I would guess maybe to just cancel out the e's and: lnfx = xlnb.

And then just evaluate the derivative: (lnfx)' = (xlnb)'

i doubt this is correct, it just feels like I'm going in circles or something.

 

[SammyS]

Okay, that is kind of a tricky concept but I get it the idea of the property. I get the fact that A = e^ln(A). However in regard to the function:

s(t) = 976[.835^t - 1] + 176t

I'm trying to figure out how to apply it. The way I'm understanding this property is that it is used when trying to eliminate a log from an equation.

...

No.

It's used so that you have e^t rather than 0.835^t .

Of course you can memorize: the derivative of b^t is ln(b)e^t .

 

[LearninDaMath]

No.

It's used so that you have e^t rather than 0.835^t .

Of course you can memorize: the derivative of b^t is ln(b)e^t .

Okay, so if f(x) = b^x, then its derivative equals f'x = (lnb)(b^x)

So how is it possible that f'(x) could ever equal lnb(e^x)?

In otherwords supposing b = 10, then how can ln10(10^x) be equivelent to ln10(e^x)?

EDIT: I'm sure that ln10(10^x) ≠ ln10(e^x),

So I'm trying to understand what connection I should be making.

 

[LearninDaMath]

Also, would I be raising both sides of the equation to make each side "e to the power of?" since whatever you do to one side of the equation, you do to the other.. and at what point would I apply this? Should I isolate .835^t to one side, then apply e to both sides, then take derivative? Or some other order? Or is isolating .835^t not even the way to start?

 

[SammyS]

Okay, so if f(x) = b^x, then its derivative equals f'x = (lnb)(b^x)

So how is it possible that f'(x) could ever equal lnb(e^x)?

In otherwords supposing b = 10, then how can ln10(10^x) be equivelent to ln10(e^x)?

EDIT: I'm sure that ln10(10^x) ≠ ln10(e^x),

So I'm trying to understand what connection I should be making.

Sorry about that. I had a brain cramp !

Should have been,

\displaystyle f'(x)=\ln(b)\,e^{x\,\ln(b)}=\ln(b)\,b^x​