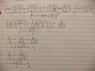SUMMARY
The discussion focuses on the differentiation of the function sec(x)/(1+tan(x)) using the quotient rule. The user initially misapplies the derivatives of sec(x) and tan(x), leading to confusion. After several iterations, the correct derivative expression is derived as ((1+tan(x))(sec(x)tan(x)) - (sec(x))(sec^2(x))) / (1+tan(x))^2. The evaluation at x=π/6 is also discussed, with simplification steps provided for clarity.
PREREQUISITES
- Understanding of trigonometric identities, specifically secant and tangent functions.
- Knowledge of the quotient rule in calculus for differentiation.
- Familiarity with evaluating trigonometric functions at specific angles, such as π/6.
- Ability to simplify algebraic expressions involving trigonometric functions.
NEXT STEPS
- Study the application of the quotient rule in calculus with examples.
- Learn about the derivatives of trigonometric functions, including sec(x) and tan(x).
- Practice evaluating trigonometric functions at various angles, focusing on π/6 and π/4.
- Explore simplification techniques for complex algebraic expressions involving trigonometric identities.
USEFUL FOR
Students studying calculus, particularly those focusing on differentiation of trigonometric functions, as well as educators seeking to clarify the application of the quotient rule.