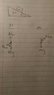Derive an expression for the acceleration of the ramp.

[Snaek96]

Homework Statement

Homework Equations

The picture is all we know about the entire system, we need to derive an expression for the acceleration of ramp M. There is no friction anywhere. The ramp is free to move on the surface beneath it.

The Attempt at a Solution

I drew the free body diagrams as such:
M: Mg pointing straight down, N_M pointing straight up, force of m on M pointing opposite of m.
m: mg pointing straight down, N_m pointing at an angle θ and 90 degrees to the incline.
System: (M+m)g pointing straight down, N_M+m pointing straight up.

I'm not sure if that's right and if it is, I don't know what to do next.

 

[Geofleur]

Note that, since the ramp does not fall through the floor or float up into the air, the sum of the vertical forces on it vanishes. Now let's focus on the block for a moment. Resolve the force on the block into two parts, one downslope and the other perpendicular to the ramp. One of these translates into a force on the ramp and causes the ramp to move - which one is it? See if you can draw a free body diagram for the ramp now. Can you resolve the force of the block on the ramp further in any useful way?

And one more thing: Once you have a formula for the acceleration, see if it gives the right answers for $\theta = 0$ and $\theta = 90^{\circ}$.

 

[Snaek96]

these are my free body diagrams. is there anything I'm missing?

 

[Geofleur]

Looks right to me, only I would label the force of the block on the ramp a little differently, to distinguish it from the normal force on the block. For example, one could write $\mathbf{F}_{BR}$ for the force of the Ramp on the Block, and $\mathbf{F}_{RB}$ for that of the Block on the Ramp. Then, of course, $\mathbf{F}_{BR} = -\mathbf{F}_{RB}$, as your picture suggests. Now resolve $\mathbf{F}_{RB}$ into a horizontal and vertical part. Which part are we interested in?

 

[Snaek96]

The x direction. I need to know which way the direction of the acceleration is for the ramp and block. I know the direction of acceleration for the ramp is to the left but I get confused when thinking about the block because depending on the frame of reference, it could be down the incline or to the bottom left.

 

[Geofleur]

Now that we have the free body diagram for the ramp, we can focus on just those forces. The force of the block on the ramp has a horizontal part and a vertical part. The vertical part plus the weight of the ramp is canceled by the normal force on the block due to the floor. Can you come up with an expression for the horizontal part in terms of the weight of the block?