Alexanddros81
- 177
- 4
Homework Statement
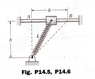
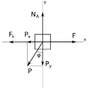
14.6 The coefficient of kinetic friction between the slider and the rod is μ, and the
free length of the spring is ##L_0 = b##. Derive the expression for the work done by
the friction force on the slider as it moves from A to B. Neglect the weight of the slider.
Homework Equations
The Attempt at a Solution
I[/B] am going the right direction with my solution?
I don't see to be getting the ##-0.1186μkb^2## solution.