Matejxx1
- 72
- 1
- Homework Statement
- Determine the motion of yoyos for $n=1,2,3$
- Relevant Equations
- ##J=\frac{mr^2}{2}##
##J\ddot\theta=Fr##
I have trouble solving this problem any help would be appreciated.Problem statement
##J=\frac{mr^2}{2}##
a) Determine the motion of yoyos for ##n=1,2,3##
The case for ##n=1## is simple, however, I am having trouble with ##n=2## and ##n=3##.
for ##n=2## I started by drawing all the forces:
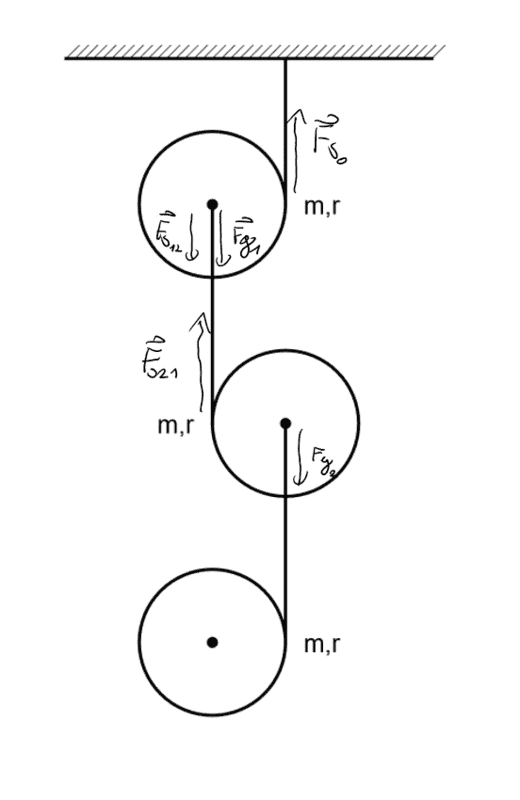
and then I wrote out the equations of motions.
##1## yoyo:
$$
m\ddot{x_1}=F_{g_{1}}+F_{s_{12}}-F_{s_{0}}$$
$$
J\ddot\theta_{1}=F_{s_{0}}r
$$
##2## yoyo:
$$
m\ddot{x_2}=F_{g_{2}}-F_{s_{21}}$$
$$
J\ddot\theta_{2}=F_{s_{21}}r
$$
What I wanted to do here was also introduce a constraint ##\dot{x_{2}}=\dot{x_{1}}+\dot\theta_{2}r##, however, I am not sure whether this is correct. It feels right because the speed of the 2nd one is going to depend on how fast the 2nd yoyo spins and how fast the 1st one moves. From here I continued
$$
\ddot\theta_{1}r=\ddot{x_{1}} \hspace{2cm} J\ddot\theta_{1}=F_{s_{0}}r\implies F_{s_{0}}=\frac{J}{r^2}\ddot{x_{1}}$$
$$
\ddot\theta_{2}r=\ddot{x_{2}}-\ddot{x_{1}}\implies\ddot\theta_{2}=\frac{\ddot{x_{2}}-\ddot{x_{1}}}{r}\implies F_{s_{21}}=\frac{J(\ddot{x_{2}}-\ddot{x_{1}})}{r^2}
$$
Plugging both forces into the equations of motions and using that ##|F_{s_{21}}|=|F_{s_{12}}|## I got
$$
m\ddot{x_1}=F_{g_{1}}+F_{s_{12}}-F_{s_{0}}\implies m\ddot{x_1}=mg+\frac{J(\ddot{x_{2}}-\ddot{x_{1}})}{r^2}-\frac{J}{r^2}\ddot{x_{1}} $$
$$
m\ddot{x_2}=F_{g_{2}}-F_{s_{21}}\implies m\ddot{x_2}=mg-\frac{J(\ddot{x_{2}}-\ddot{x_{1}})}{r^2}
$$
Plugging in ##J=\frac{mr^2}{2}##$$
m\ddot{x_1}=mg+\frac{m(\ddot{x_{2}}-\ddot{x_{1}})}{2}-\frac{m}{2}\ddot{x_{1}} $$
$$
m\ddot{x_2}=mg-\frac{m(\ddot{x_{2}}-\ddot{x_{1}})}{2}
$$
diving by ##m##$$
\ddot{x_1}=g+\frac{(\ddot{x_{2}}-\ddot{x_{1}})}{2}-\frac{1}{2}\ddot{x_{1}} \implies 2\ddot{x_1}-\frac{1}{2}\ddot{x_{2}}=g$$
$$
\ddot{x_2}=g-\frac{(\ddot{x_{2}}-\ddot{x_{1}})}{2}\implies\frac{3}{2}\ddot{x_{2}}-\frac{1}{2}\ddot{x_{1}}=g
$$
From here on its easy to find out ##\ddot{x_{1}}## and ##\ddot{x_{2}}##. However, I am not sure whether the way I did it is correct. I am unsure if the constraint ##\dot{x_{2}}=\dot{x_{1}}+\dot\theta_{2}r## really need to be there and I am also unsure how to go on from here to ##n=3## and for general ##n\in \mathbb{N}##.
##J=\frac{mr^2}{2}##
a) Determine the motion of yoyos for ##n=1,2,3##
The case for ##n=1## is simple, however, I am having trouble with ##n=2## and ##n=3##.
for ##n=2## I started by drawing all the forces:
and then I wrote out the equations of motions.
##1## yoyo:
$$
m\ddot{x_1}=F_{g_{1}}+F_{s_{12}}-F_{s_{0}}$$
$$
J\ddot\theta_{1}=F_{s_{0}}r
$$
##2## yoyo:
$$
m\ddot{x_2}=F_{g_{2}}-F_{s_{21}}$$
$$
J\ddot\theta_{2}=F_{s_{21}}r
$$
What I wanted to do here was also introduce a constraint ##\dot{x_{2}}=\dot{x_{1}}+\dot\theta_{2}r##, however, I am not sure whether this is correct. It feels right because the speed of the 2nd one is going to depend on how fast the 2nd yoyo spins and how fast the 1st one moves. From here I continued
$$
\ddot\theta_{1}r=\ddot{x_{1}} \hspace{2cm} J\ddot\theta_{1}=F_{s_{0}}r\implies F_{s_{0}}=\frac{J}{r^2}\ddot{x_{1}}$$
$$
\ddot\theta_{2}r=\ddot{x_{2}}-\ddot{x_{1}}\implies\ddot\theta_{2}=\frac{\ddot{x_{2}}-\ddot{x_{1}}}{r}\implies F_{s_{21}}=\frac{J(\ddot{x_{2}}-\ddot{x_{1}})}{r^2}
$$
Plugging both forces into the equations of motions and using that ##|F_{s_{21}}|=|F_{s_{12}}|## I got
$$
m\ddot{x_1}=F_{g_{1}}+F_{s_{12}}-F_{s_{0}}\implies m\ddot{x_1}=mg+\frac{J(\ddot{x_{2}}-\ddot{x_{1}})}{r^2}-\frac{J}{r^2}\ddot{x_{1}} $$
$$
m\ddot{x_2}=F_{g_{2}}-F_{s_{21}}\implies m\ddot{x_2}=mg-\frac{J(\ddot{x_{2}}-\ddot{x_{1}})}{r^2}
$$
Plugging in ##J=\frac{mr^2}{2}##$$
m\ddot{x_1}=mg+\frac{m(\ddot{x_{2}}-\ddot{x_{1}})}{2}-\frac{m}{2}\ddot{x_{1}} $$
$$
m\ddot{x_2}=mg-\frac{m(\ddot{x_{2}}-\ddot{x_{1}})}{2}
$$
diving by ##m##$$
\ddot{x_1}=g+\frac{(\ddot{x_{2}}-\ddot{x_{1}})}{2}-\frac{1}{2}\ddot{x_{1}} \implies 2\ddot{x_1}-\frac{1}{2}\ddot{x_{2}}=g$$
$$
\ddot{x_2}=g-\frac{(\ddot{x_{2}}-\ddot{x_{1}})}{2}\implies\frac{3}{2}\ddot{x_{2}}-\frac{1}{2}\ddot{x_{1}}=g
$$
From here on its easy to find out ##\ddot{x_{1}}## and ##\ddot{x_{2}}##. However, I am not sure whether the way I did it is correct. I am unsure if the constraint ##\dot{x_{2}}=\dot{x_{1}}+\dot\theta_{2}r## really need to be there and I am also unsure how to go on from here to ##n=3## and for general ##n\in \mathbb{N}##.