Frames of Reference: Linear Acceleration View
My previous Insight, Frames of Reference: A Skateboarder’s View, explored mechanical energy conservation as seen from an inertial frame moving relative to the “fixed” Earth. Shifting one’s point of view to the moving frame proved to be somewhat controversial as far as mechanical energy conservation was concerned. Here I will examine shifting into accelerating frames as a means of simplifying solutions to certain problems. I will limit the discussion to frames undergoing linear acceleration, a topic that is not as extensively covered in textbooks as rotating frames. I hope to convince the reader that shifting one’s frame of reference to a linearly accelerating frame reveals hidden gems of the “I never thought of it that way” variety.
Table of Contents
Apparent gravity
The rule for transforming into a linearly accelerating frame of reference is simple: Draw a free body diagram as if the system of mass ##m## were in an inertial frame, add the fictitious force ##-m \vec{a}## to all the other forces and put yourself in that frame by declaring your acceleration to be zero. Any force that you feel must be a contact force that keeps you at rest against gravity. Thus, the sum of all the forces and ##-m \vec{a}## divided by the mass becomes the apparent acceleration of gravity, ##\vec{g}_{app.}## This may seem like a trivial result for all it does is move the right side of Newton’s second law equation from the right side to the left. Yet, it often provides a convenient and simplified way of looking at the world. In what follows, ##\vec{g}_0## denotes the constant acceleration of gravity, ##9.8~\rm{m/s^2}## towards the center of the Earth.
Example 1
Alice and Bob stand on two different floors of a tall building. They throw two balls straight up at the same time. The balls rise to their respective maximum heights, come back down and land on the ground below at the same time. Excluding the time when the balls hit the ground, how many times do the balls cross paths?
- Zero.
- One.
- Two.
- It depends.
The correct answer may be obtained by the “brute force” method of writing kinematics equations for the position of each ball, then finding an expression for the distance between them and, finally, finding at what time(s) this distance is zero. That the answer is “zero” can be seen immediately if one transforms to the accelerated frame of either ball. In that frame, the apparent acceleration of gravity is zero and the balls move towards each other at constant relative speed. Two balls moving towards each other at constant speed can only cross paths once, in this case when they land on the ground.
Incidentally, transforming to the accelerating frame provides an explanation without equations to the familiar shoot the monkey lecture demonstration. The initial velocity of the projectile, also the initial projectile velocity relative to the monkey, is directed straight towards the monkey. Because the monkey and the projectile are in free fall, their velocities change in exactly the same way at all subsequent times. Therefore, the relative velocity will remain directed at the monkey until the collision.
Example 2
Bob has lived all his life in a train car accelerating to the right with acceleration a. Alice can look inside the train car but Bob cannot see what’s outside it. What does each observer see?
Alice’s view
(a) Bob is holding a plumb bob in his hand. In what direction, relative to the vertical, does Alice see the plumb bob hang? Answer: The string is tilted down and to the left. The tension in the string has adjusted itself so that its vertical component matches the weight, ##T \cos\theta = mg_0##. The horizontal component of the tension provides the observed acceleration, ##T \sin\theta = ma##. The angle relative to the vertical is given by ##\tan \theta = a/g_0##.
(b) Bob is holding a helium balloon in his hand. In what direction does Alice see the balloon float? Answer: The balloon floats in a direction opposite to the plumb bob, up and to the right. The plumb bob and balloon strings are parallel.
Bob’s view
(a) Bob is holding a plumb bob in his hand. In what direction, relative to the vertical, does Bob see the plumb bob hang? Answer: Straight down because plumb bobs, by definition, point down.
(b) Bob is holding a helium balloon in his hand. In what direction does Bob see the balloon pull on its string? Answer: Straight up, as all tethered helium balloons do when there is no wind. “Up” is opposite to “down”, i.e. the tension holding the balloon is opposite to the tension holding the plumb bob. The plumb bob and balloon strings are parallel.
Having been in the train car all his life, Bob has made it livable. He knows he is on an inclined plane because the plumb bob is not perpendicular to the floor. The incline forms angle ##\alpha## with respect to his horizontal which lies in the plane perpendicular to his plumb bob. In terms of the acceleration ##a##,
$$\sin \alpha = \frac{a}{\sqrt{a^2+g_0^2}}; \ \ \cos \alpha = \frac{g_0}{\sqrt{a^2+g_0^2}}$$
Bob has measured the acceleration of gravity to be ##g_{app.}=\sqrt{g_0^2+a^2}##. He has duly used his plumb bob to build a wall separating his living quarters from his lab with steps leading up to it. There is a table in the lab with a ballistic cart resting on it. The cartoon below shows Alice’s view of Bob’s world as he zooms by (left) and Bob’s world as he sees it (right). Although both pictures are equivalent, Bob’s view probably looks “more correct” to the reader. Because of the ingrained assumption in the reader’s mind that the acceleration of gravity points from the top of the screen to the bottom, Bob’s view looks reasonable as a snapshot of static equilibrium whereas Alice’s does not. The ballistic cart in Bob’s lab is “obviously” at rest (right picture), but it “has to” roll down the table in the left picture. Let us now look into the ballistic cart a little more in detail.
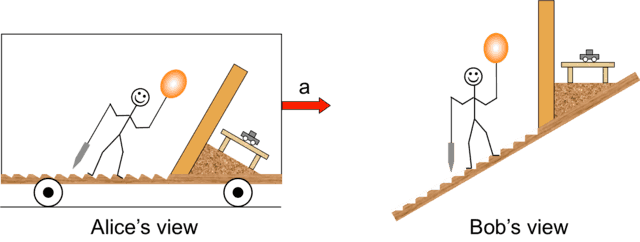
The ballistic cart
The ballistic cart rides on a track and can shoot a ball straight away from it in a direction perpendicular to the direction of its motion. In the conventional demonstration, the cart is started moving on its track horizontally. A tab mounted on the track triggers a photogate on the cart that releases a cocked spring launching the ball in the air. The ball describes a parabolic trajectory and falls back in the cup farther down the track.
To explain this, one might say something like, “after launch, the horizontal velocity of both ball and cart, which are initially the same, stay the same. Therefore, the ball is directly above the cup at all times and eventually falls back in it.” However, although not incorrect, this explanation may lead to an unwarranted generalization. Suppose we ask, What if the horizontal velocity of the cart changes while the ball is in the air? Based on the explanation, one may reasonably conclude that the ball will not fall in the cup. However, this is not necessarily the case. As a counterexample, consider the ballistic cart placed on an inclined track and given a push. It so happens that the launched ball will again fall back in the cup regardless of the direction of the motion. The following short video demonstrates this.
Clearly, in the horizontal direction, the velocity of the cart changes while the velocity of the ball does not. What’s going on? The acceleration of the cart is ##a_x=g_0 \sin \theta## downhill. If we transform to “cart Bob’s” frame of reference, the apparent acceleration of gravity is perpendicular to the track with magnitude ##g_{app.}=g_0 \cos \theta## as illustrated in the diagram below.
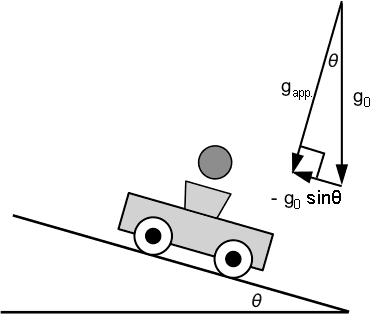
From “cart Bob’s” perspective, the ball is shot straight up and falls straight back down. Thus, the appropriate explanation for the ballistic cart is “the ball falls back in the cup because the component of the ball’s velocity in the direction of motion of the cart changes in exactly the same way as the cart’s velocity.” In other words, the relative velocity between the ball and the cart must have a zero component in the direction of motion of the cart at all times. The ball will fall back in the cup at any incline angle ##\theta##, the horizontal case ##\theta = 0## being only a special case.
We now see that “train Bob” can perform the ballistic cart demonstration on his lab table or the (inclined) floor of his residence or an incline of his choosing and the ball will always fall in the cup. Same with Alice. But wait! There is more.
Thinking heuristically outside the cart
Consider the following problem: A projectile is shot downhill at angle ##\varphi## relative to the surface of a plane inclined at angle ##\theta## relative to the horizontal. Find the downhill range R.
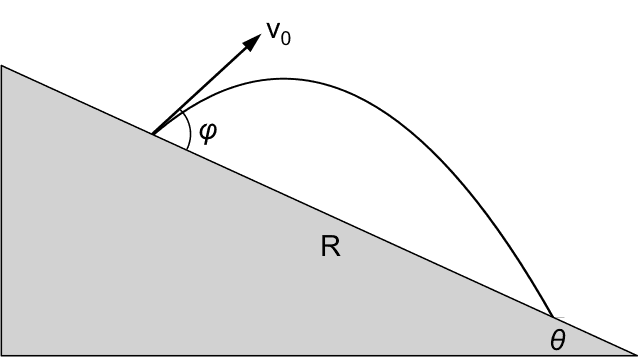
Solution
The traditional approach involves writing the kinematics equations in the horizontal and vertical direction and then cranking out the algebra. This approach is rather involved and requires finding the two points of intersection of a straight line and a parabola. Instead, we model the problem as if the projectile were shot from a ballistic cart rolling down the incline with velocity ##v_{0x}=v_0 \cos \varphi## at the time of launch. (Downhill is the positive x-axis.) To match the projectile’s given initial velocity, the cart is released from rest far enough uphill so that its downhill velocity is ##v_{0y}=v_0 \sin \varphi## when it reaches the trigger. The time of flight can be conveniently found in the accelerated frame where the apparent acceleration of gravity is ##g_{app.}=g_0 \cos \theta##. We have seen that, in this frame, the ball goes straight up and falls straight back down. Its time of flight is $$t_f=\frac{\Delta v_{0y}}{g_{app.}}=\frac{2v_0 \sin \varphi}{g_0 \cos \theta}$$
Going back to the inertial frame of the incline, in time ##t_f## the cart travels a distance given by the standard kinematic equation
$$R=v_0 \cos \varphi \ t_f+\frac{1}{2}g_0 \sin \theta \ t_f^2.$$
Using the expression for ##t_f##, simple algebra and a trig identity, we arrive at
$$R=\frac{2 v_0^2 \sin \varphi \cos (\theta – \varphi)}{g_0 \cos^2 \theta}.$$
A generalization
Consider the position vector at time ##t## of a projectile launched from the origin, with motion taking place in the xy-plane,
$$\vec{r}= \vec{v}_0~t-\frac{1}{2}g_0t^2 \hat{y}$$
A unit vector in the direction of the position vector is $$\hat{r}=\frac{x\hat{x}+y\hat{y}}{r}$$ and a unit vector perpendicular to ##\hat{r}## (in the “up” direction) is $$\hat{n}=\frac{ -y\hat{x}+x\hat{y}}{r}$$
We now consider a hypothetical ballistic cart that, at t = 0, launches the ball and starts rolling on an incline along ##\vec{r}##. The cart has the right initial velocity to reach the tip of the position vector in just the right time t to catch the ball. Let ##\alpha## be the angle of the incline (and the position vector) relative to the horizontal. Then ##\cos \alpha = x/r##. As we have seen, according to “cart Bob” the time (of flight) to point {x, y} is
$$t=\frac{2~\vec{v}_0 \cdot \hat{n}}{g_0 \cos \alpha}=\frac{2~v_0~(-y \cos \theta +x \sin \theta)}{g_0 x}$$
It relates the elapsed time, the coordinates {x, y} of the instantaneous position vector and the initial velocity vector and is valid in all cases. Note that this expression can be used to eliminate the independent variable t from the projectile motion equations to obtain new equations to be used for solving projectile problems without going through the time of flight. For example, the problem of finding the horizontal range ##R## of a projectile fired from the edge of a cliff of height ##h## requires solving the quadratic in ##R##,
$$R=v_0 \cos \theta \times \frac{2~v_0~(h \cos \theta +R \sin \theta)}{g_0 R}.$$
The physically meaningful solution of the two is modeled with the ballistic cart rolling down the incline. The rejected solution, which corresponds to the projectile being fired so that it reaches height ##h## with velocity ##\vec{v}_0##, can be modeled with the ballistic cart rolling up the incline. In the interests of brevity, the details are left as an exercise to the reader.
I am a retired university physics professor. I have done research in biological physics, mostly studying the magnetic and electronic properties at the active sites of biomolecules and their model complexes. I have also dabbled in Physics Education research.






There have been a couple of problems in the homework forums where there is a collision either in mid air or an inclined plane. In these situations I have advised that normal collision dynamics will apply since the colliding bodies are in the same "linearly accelerating frame". Would this be correct? See for eg:
https://www.physicsforums.com/threads/collision-in-a-free-fall.714625/#post-6087213
and
https://www.physicsforums.com/threa…ollision-going-up-a-ramp.959006/#post-6081332
Great uses of media and diagrams!