Designing NFA & DFA for (1001 + 110 + 11)* Language

[Lolligirl]

Hello everyone! I'm trying to design an NFA and then turn it into a DFA, and I'm not sure if I've done it correctly so far. Here is the question:

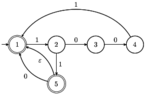
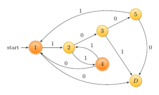
"Present a transition diagram for an NFA for the language associated with the regular expression (1001 + 110 + 11)*. Your NFA must have no more than five states. Then, use the standard conversion technique (subsets of states) to convert the NFA to an equivalent DFA. Be sure to not include unreachable states. Hint: This DFA should have no more than six states."

And here is my attempt at an answer:

View attachment 3147

Would this work as the NFA or DFA? I feel like I'm missing something here, but I am not sure what. Any help is appreciated! :D

 

[Evgeny.Makarov]

Hi, and welcome to the forum!

Your automaton accepts 111 and 10, which are not in the original language. How about the following NFA?

View attachment 3151

 

[Lolligirl]

Oh, I see! Thank you so much for pointing that out, Evgeny: I indeed included the string 10!

Okay, so now I understand the NFA, but I guess I really don't understand what's going on with the epsilon there. Why, from state 5 in the diagram, are we going back to state 1 on epsilon? Also, is that the only thing making this an NFA and not a DFA? As far as I can tell, state 2, for instance, indeed can branch two different ways, but there's only one character per arrow. So I guess my question is basically, what makes this not a DFA already besides the epsilon?

Sorry if this is dead simple! >.<

 

[Evgeny.Makarov]

Just to avoid confusion: $\varepsilon$ denotes the empty word, which is also sometimes denoted by $\lambda$. Going from an accepting state back to the initial one on $\varepsilon$ is a usual thing in an automaton accepting $L^*$ for some $L$. This is how we show that the set of languages accepted by NFAs is closed under the Kleene star. In this case, both 11 and 110 should lead to the initial state, which is the reason for the two arrows from 5 to 1.

Yes, $\varepsilon$ makes it an NFA, but also not all states have outgoing arrows for both 0 and 1. In a DFA, the transition function has to be total, i.e., defined on all pairs from $Q\times\Sigma$. If it were not for the $\varepsilon$ arrow, to turn this automaton into a DFA one needs to add a sink state with all the missing arrows going there. By the way, I did not draw a 1-arrow from 2 to 1 because then it's not clear what to do with the word 110 since 0 should be accepted only after two 1's.

 

[Lolligirl]

Ohh! By a sink state, do you mean like a dead state? So would it be kind of like this (D for dead)?

https://dl.dropboxusercontent.com/u/5778771/Assignment3Number1.jpg

Either way, thank you so much, Evgeny; I really feel like I'm starting to get it! :D

 

[I like Serena]

Let's make that:

View attachment 3161

Since $11$ should be accepted.
And since after $11$ we can get something that starts with a $1$.

 

[Lolligirl]

Right, right, of course! That makes much more sense now; thank you very much for helping me understand, Evgeny, en hartelijk bedankt, I like Serena! :D