Detecting Mass Changes with a Hydraulic Balance

[tacoman326]

A hydraulic balance used to detect small changes in mass is shown in Fig. 9.31. If a mass m of 0.40 g is placed on the balance platform, by how much will the height of the water in the smaller, 1.0 cm diameter cylinder have changed when the balance comes to equilibrium?

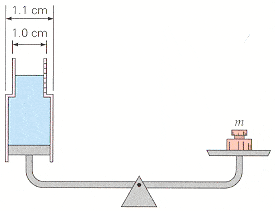
please give a detailed explanation. thanks I now know the answer for the question is (4.21 mm)

 

[alwynj]

Are you certain you have the problem correct?

The balance is simply balancing the weight of the water against the weight of the mass m.
If they are not equal there will be no equilibrium assuming no friction and it is on a planet.

 

[Phrak]

Odd that your diagram indicate the outside diameters of the cylinders, rather than the inside diameters.

 

[Georgepowell]

Are you certain you have the problem correct?

The balance is simply balancing the weight of the water against the weight of the mass m.
If they are not equal there will be no equilibrium assuming no friction and it is on a planet.

Odd that your diagram indicate the outside diameters of the cylinders, rather than the inside diameters.

I think the diagram is very simplified. I think you can presume the frame in which the water is being held is fixed relative to the pivot. And that the dimensions are from the inside of the container. There are other problems I could point out if I was being pedantic, but just presume it is simplified.

Am I right?

I don't know how to answer this question tbh, but I am interested in the answer.

 

[Phrak]

I think the diagram is very simplified. I think you can presume the frame in which the water is being held is fixed relative to the pivot. And that the dimensions are from the inside of the container. There are other problems I could point out if I was being pedantic, but just presume it is simplified.

Am I right?

Sounds right to me.

I don't know how to answer this question tbh, but I am interested in the answer.

On second glance, it's actually a clever device. Whether it's practicle or not would depend upon how much friction there would be between cylinder and piston.

As to the answer, notice that an amplification effect is obtained from the ratio of the two cylinder diameters. If the piston is moved 5 cm, the overall height of the column of water changes about 1 cm, as it is squeezed into the upper cylinder.

Given a balance with two equal arms, the delta-weight (in grams) is equal to the change in height of the water column times the piston area.

The answer will be the displacement of the cylinder plus the change in height of the water column; about 6 cm per gm, I think.

 

[Carid]

Given a balance with two equal arms, the delta-weight (in grams) is equal to the change in height of the water column times the piston area.


I think we'll need the density of water in there too.

DeltaHeight x WaterDensity x PistonArea = DeltaWeight