Determine angular velocity - Dynamics

AI Thread Summary
The discussion focuses on determining the angular velocity of a bar connected to a torsional spring as it moves from a horizontal to a vertical position. Participants emphasize the importance of applying the conservation of energy principle, identifying three types of energy: elastic potential energy, gravitational potential energy, and rotational kinetic energy. The correct approach involves calculating the initial and final energies, ensuring to account for the change in gravitational potential energy as the center of mass rises. The calculations lead to the conclusion that the rotational kinetic energy at the vertical position can be derived from the total energy, allowing for the determination of angular velocity. The moment of inertia for the bar is also clarified as I = 1/3mL^2 for accurate calculations.
dvep
Messages
43
Reaction score
0

Homework Statement



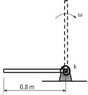
Torsional spring constant k=33 Nm/rad
It is undeflected when it is in the vertical position, it weighs 6.4 kg
When the bar is released from the horizontal position from rest, determine the angular velocity \omega as it passess the vertical position.
We can assume that it is frictionless.

The Attempt at a Solution



Am I right to say that I have to use the conservation of energy and find

T1+V1 = T2+V2 which would be my angualr velocity?

I am quite stuck on this question, I would be grateful for some guidance.
 

Attachments

  • Untitled1.jpg
    Untitled1.jpg
    2.1 KB · Views: 530
Last edited:
Physics news on Phys.org
Yes, you'll need to apply conservation of energy. Hint: There are three 'types' of energy involved here. What are they? What are expressions for each?
 
Doc Al said:
Yes, you'll need to apply conservation of energy. Hint: There are three 'types' of energy involved here. What are they? What are expressions for each?

Thank you for your reply

Elastic potential energy = 1/2kx^2
Rotational kinetic energy = 1/2Iw^2 = 1/2I(v/r)^2

Though I am unsure what the third energy is.

So,

EPE=1/2*33*(0.8/sin45)^2 = 20 J

Am I on the right track?

Sorry to be a pain, I haven't been taught this yet in class.
 
dvep said:
Thank you for your reply

Elastic potential energy = 1/2kx^2
OK, but for a torsion spring, the displacement from equilibrium will be in radians.
Rotational kinetic energy = 1/2Iw^2 = 1/2I(v/r)^2
OK.

Though I am unsure what the third energy is.
Hint: The bar has weight.

So,

EPE=1/2*33*(0.8/sin45)^2 = 20 J
Not sure what you did here. What angle (in radians) does the initial position make with the unstretched position?
 
doc al said:
ok, but for a torsion spring, the displacement from equilibrium will be in radians.

Oh yeah, so

EPE=1/2k\theta^2

doc al said:
hint: The bar has weight.

I wasn't sure but I was thinking gravitational potential energy?

doc al said:
not sure what you did here. What angle (in radians) does the initial position make with the unstretched position?

EPE=1/2*33*1.571^2 J
 
dvep said:
Oh yeah, so

EPE=1/2k\theta^2
Right.

I wasn't sure but I was thinking gravitational potential energy?
Exactly.

EPE=1/2*33*1.571^2 J
Good.
 
Doc Al said:
Right.


Exactly.


Good.

So,

EPE=40.723 J
GPE=50.176 J

Am I meant to add these together to get the total energy, then at the vertical position they both equal 0 and rotational kinetic energy equals the total energy, then use the rotational kinetic energy formula and rearrange to find the angualr velocity w?
 
dvep said:
EPE=40.723 J
OK.
GPE=50.176 J
How did you calculate this? For what position? Initial or final?

Am I meant to add these together to get the total energy, then at the vertical position they both equal 0 and rotational kinetic energy equals the total energy, then use the rotational kinetic energy formula and rearrange to find the angualr velocity w?
To avoid confusion, set up your conservation equation like so:

EPE1 + GPE1 + RotKE1 = EPE2 + GPE2 + RotKE2

(Some terms will end up being zero.)
 
Doc Al said:
How did you calculate this? For what position? Initial or final?

I thought that might be wrong

GPE1=mglcos(theta)= 6.4*9.8*0.8*cos(1.571) = 50.157 J
GPE2=mglcos(theta)= 6.4*9.8*0.8*cos(0) = 50.157 J

Is that correct, they are both the same.

Doc Al said:
To avoid confusion, set up your conservation equation like so:

EPE1 + GPE1 + RotKE1 = EPE2 + GPE2 + RotKE2

(Some terms will end up being zero.)

So what I get,

EPE1 + GPE1 + RotKE1 = EPE2 + GPE2 + RotKE2
40.723 + 50.157 + 0 = 0 + 50.157 + 40.723

RotKE2= 1/2Iw^2 = 1/2I(v/r)^2
Angular velocity = w = sqrt(2*RotKE2/mr^2) = sqrt(2*40.723/6.4*0.8^2) = 4.459 rads/s

Am I at least a little bit close?
 
  • #10
dvep said:
I thought that might be wrong

GPE1=mglcos(theta)= 6.4*9.8*0.8*cos(1.571) = 50.157 J
GPE2=mglcos(theta)= 6.4*9.8*0.8*cos(0) = 50.157 J

Is that correct, they are both the same.
No, that makes no sense. The bar rises from horizontal to vertical, so its GPE increases. Hint: Measure height from the surface. Hint 2: Consider what happens to the center of mass.
 
  • #11
Doc Al said:
No, that makes no sense. The bar rises from horizontal to vertical, so its GPE increases. Hint: Measure height from the surface. Hint 2: Consider what happens to the center of mass.

I'm still lost. What do you mean measure the height from the surface? Will the center of mass move towards the end of the bar?
 
  • #12
dvep said:
I'm still lost. What do you mean measure the height from the surface? Will the center of mass move towards the end of the bar?
When the bar goes from horizontal to vertical, what happens to its center of mass? That determines the change in gravitational PE.
 
  • #13
Doc Al said:
When the bar goes from horizontal to vertical, what happens to its center of mass? That determines the change in gravitational PE.

The GPE is 0 at the initial position and 50.157 J when vertical?
The center of mass gains translation kinetic energy?
 
  • #14
dvep said:
The GPE is 0 at the initial position
OK.
and 50.157 J when vertical?
No. How high does the center of mass rise?
The center of mass gains translation kinetic energy?
Sure, but you need not worry about that. Treat the bar as being in pure rotation about the axis, so all its kinetic energy is rotational KE about that axis.
 
  • #15
Doc Al said:
OK.

No. How high does the center of mass rise?

0.4 m?

so,

EPE1 + GPE1 + RotKE1 = EPE2 + GPE2 + RotKE2
40.723 + 0 + 0 = 0 + 25.088 + 15.635
 
  • #16
dvep said:
0.4 m?
Right.

so,

EPE1 + GPE1 + RotKE1 = EPE2 + GPE2 + RotKE2
40.723 + 0 + 0 = 0 + 25.088 + 15.635
OK, but since you are solving for RotKE2, I'd write it as:
EPE1 + GPE1 + RotKE1 = EPE2 + GPE2 + RotKE2
40.723 + 0 + 0 = 0 + 25.088 + RotKE2

Then you'd deduce that RotKE2 = 15.635

And then use RotKE = 1/2Iw^2 to find w.
 
  • #17
Doc Al said:
Right.


OK, but since you are solving for RotKE2, I'd write it as:
EPE1 + GPE1 + RotKE1 = EPE2 + GPE2 + RotKE2
40.723 + 0 + 0 = 0 + 25.088 + RotKE2

Then you'd deduce that RotKE2 = 15.635

And then use RotKE = 1/2Iw^2 to find w.

Thank you for your help.
 
  • #18
Doc Al said:
Right.

Then you'd deduce that RotKE2 = 15.635

And then use RotKE = 1/2Iw^2 to find w.

Just looked through this problem... to calculate the moment of inertia, I, do you use I = 1/3mL^2?
 
  • #19
Skittles999 said:
Just looked through this problem... to calculate the moment of inertia, I, do you use I = 1/3mL^2?
Yes.
 

Similar threads

What is the final angular velocity of each cylinder
Replies
1
Views
2K
Find the height of a lamp based on the velocities of projectiles
Replies
40
Views
2K
Determine the angular velocity as a function of the angle
Replies
39
Views
3K
Angular Velocity Problem — a Piston and a Crank
Replies
12
Views
5K
Determine the angular acceleration and angular velocity
Replies
2
Views
3K
Dynamics of Rotational Motion and hinge
Replies
2
Views
3K
1D Angular Motion with different velocity stages
Replies
3
Views
2K
Simple pendulum: Determine the velocity
Replies
5
Views
1K
Find the time for the string to break
Replies
3
Views
2K
Problem in Classical Mechanics
Replies
1
Views
2K

Hot Threads

Recent Insights

Back
Top