Determine force that will cause cylinder to roll out of cart

[bkw2694]

Homework Statement

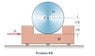
I've uploaded an image of the problem below. The problem states: Determine the value of P which will cause the homogeneous cylinder to begin to roll up out of its rectangular recess.The mass of the cylinder is m, the mass of the cart is M. Friction of the cart wheels i negligible.

Homework Equations

ΣF_x = ma_x
ΣF_y = ma_y
ΣM_G = 0

The Attempt at a Solution

I'm really not sure how to approach the cylinder in this problem, but I can see that a FBD of the problem shows m*g and M*g going downward in the y-direction, and P is in the x-direction. I'm also assuming the cart is accelerating in the x-direction, which means a_y = 0.

The correct answer is P = sqrt(3)(M+m)(g). I'm obviously missing some key force because I keep getting P =0.

 

[jbriggs444]

Have you drawn a free body diagram for the cylinder alone? What forces act on the cylinder when it is just at the verge of tipping up and out?

 

[J Hann]

The edge of the slot provides the horizontal force that accelerates the cylinder.
Generally, its best to avoid reaction forces - in this case it seems simpler to do so.
The reaction force on the C. M. provides a counter-clockwise torque about the edge of the slot.
The weight of the cylinder provides a clockwise torque about the same edge.
Obviously, once the cylinder starts to tip (torques are equal) the counterclockwise torque will exceed the clockwise torque.

 

[jbriggs444]

The edge of the slot provides the horizontal force that accelerates the cylinder.
Generally, its best to avoid reaction forces - in this case it seems simpler to do so.
The reaction force on the C. M. provides a counter-clockwise torque about the edge of the slot.
The weight of the cylinder provides a clockwise torque about the same edge.
Obviously, once the cylinder starts to tip (torques are equal) the counterclockwise torque will exceed the clockwise torque.

The approach that I have in mind is different from this. It ends with the same result but avoids talking about torque, angular momentum or reaction forces. But either way, bkw2694 needs to do that free body diagram for the cylinder alone.