- #1
Volcano
- 147
- 0
Hi,
I hope asking in right forum.
I'm trying to understand proper time concept but I'm afraid couldn't understand the reason of answer for below question.
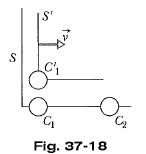
"Figure 37-18 shows two clocks in stationary frame S (they are syncronized in that frame) and one clock in moving frame S'. Clocks C1 and C1' read zero when they pass each other. When clock C1' and C2 pass each other,
(a) Which clock has the smaller reading
and
(b) which clock measures a proper time?
"
What I couldn't understand here is, how can I determine the observer in this type of question. I'm sure those clocks giving the hints about events but how? And yes, (a) and (b) asking the same thing. Proper time always smaller.
I hope asking in right forum.
I'm trying to understand proper time concept but I'm afraid couldn't understand the reason of answer for below question.
"Figure 37-18 shows two clocks in stationary frame S (they are syncronized in that frame) and one clock in moving frame S'. Clocks C1 and C1' read zero when they pass each other. When clock C1' and C2 pass each other,
(a) Which clock has the smaller reading
and
(b) which clock measures a proper time?
"
What I couldn't understand here is, how can I determine the observer in this type of question. I'm sure those clocks giving the hints about events but how? And yes, (a) and (b) asking the same thing. Proper time always smaller.