Differential Cartesian Coordinates Into Cylindrical Coordinates

Click For Summary
SUMMARY

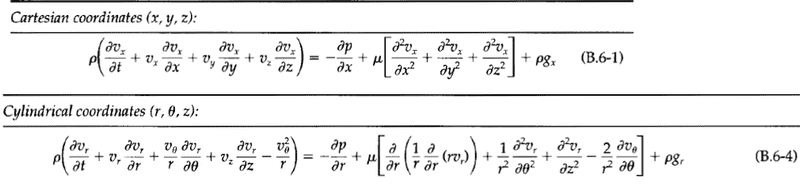
The discussion focuses on converting differential Cartesian coordinates into cylindrical coordinates, specifically in the context of the transport phenomenon as outlined in "Source Transport Phenomenon 2nd ed." The user seeks assistance in transforming the velocity components from Cartesian (Vx, Vy, Vz) to cylindrical coordinates (Vr, Vθ, Vz). The key relationships established include Vx = Vr * Cos(θ) and Vy = Vr * Sin(θ), but the user requires further guidance on deriving the angular component Vθ.

PREREQUISITES
  • Understanding of differential equations in fluid dynamics
  • Familiarity with coordinate transformations
  • Knowledge of cylindrical coordinate systems
  • Basic grasp of vector components in physics
NEXT STEPS
  • Study the derivation of velocity components in cylindrical coordinates
  • Learn about the application of the transport equation in fluid mechanics
  • Research the mathematical principles behind coordinate transformations
  • Explore examples of converting between Cartesian and cylindrical coordinates
USEFUL FOR

Students and professionals in engineering, particularly those specializing in fluid dynamics, as well as anyone involved in solving transport phenomena problems.

sorter
Messages
47
Reaction score
0
Has to convert B6-1 into B6-2 Source Transport Phenomenon 2nd ed -

sxgd39.jpg
 
Physics news on Phys.org
I can't even start solution
No idea how to convert subscipt from vx to vr and or to vtheta?
 
You are to find the radial component of the transport equation.

Set up the relevant quantities and relationships, then we'll help you.
 
In the first equation: substitute Vx = Vr * Cos (theta) Vy = Vr * Sin (theta) Vz = Vz

but how do I get V(theta)
 

Thread 'Distance between a Clock's hands when the distance is increasing most rapidly'

Question: A clock's minute hand has length 4 and its hour hand has length 3. What is the distance between the tips at the moment when it is increasing most rapidly?(Putnam Exam Question) Answer: Making assumption that both the hands moves at constant angular velocities, the answer is ## \sqrt{7} .## But don't you think this assumption is somewhat doubtful and wrong?
View full post »

Similar threads

Recast a given vector field F in cylindrical coordinates
  • · Replies 4 ·
Replies
4
Views
2K
Volume of a sphere in cylindrical coordinates
  • · Replies 6 ·
Replies
6
Views
3K
Change integration limits for cylindrical to cartesian coord
  • · Replies 1 ·
Replies
1
Views
2K
How to set bounds in cylindrical coordinates analytically?
  • · Replies 4 ·
Replies
4
Views
2K
Finding the Basis Vectors for a Coordinate System
  • · Replies 6 ·
Replies
6
Views
3K
Sketching surfaces described in cylindrical coordinates
  • · Replies 17 ·
Replies
17
Views
4K
Cartesian to Cylindrical coordinates?
  • · Replies 6 ·
Replies
6
Views
3K
Hollow Sphere Inertia in Cartesian Coordinates
  • · Replies 4 ·
Replies
4
Views
2K
Integration of acceleration in polar coordinates
  • · Replies 24 ·
Replies
24
Views
3K
Laplace in Spherical and Cylindrical Coordinates
  • · Replies 1 ·
Replies
1
Views
2K