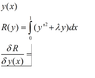Differential under an integral sign.

[binbagsss]

Sorry I'm not sure how you get math script on here, so have had to attach it.

It is a differential under an integral sign and I'm not too sure how to approach it.
Would you use Leibniz rule?
Do you differentiate or integrate first?
- where y is a function of x, and R of y

Thanks in advance

 

[STEMucator]

You don't need to integrate here.

You have y as a function of x and R as a function of y. You want to find the partial of R with respect to y which you know is a function of x. So when you differentiate the integrand, don't forget to apply the chain rule.

 

[vanhees71]

No! What's asked for is the functional derivative. You get it by evaluating, how the integral changes when the function $y(x)$ changes by an infinitesimal $\delta y(x)$. Unfortunately the problem is not completely stated. You also need boundary conditions. If it's a usual variational problem like in Hamilton's principle, the values at the end points are fixed.