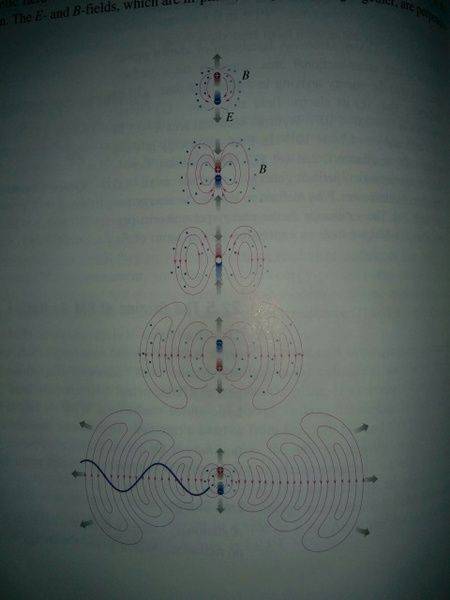
Though shalt not make images ;-)). Just calculate the the electric dipole field, using the retarded potential. For a plane-wave mode of frequency ##\omega## it leads to an electric field,
$$\vec{E}(t,\vec{r})=\vec{E}'(\vec{r}) \exp(-\mathrm{i} \omega t)$$
with
$$\vec{E}'(\vec{r})=\frac{q}{4 \pi r^3} \left [\frac{3-\mathrm{i} k r-k^2 r^2}{r^2} \vec{r} (\vec{r} \cdot \vec{d})-(1-\mathrm{i} k r - k^2 r^2)\vec{d} \right ] \exp(\mathrm{i} k r),$$
$$\vec{B}'(\vec{r})=-\frac{\mathrm{i}k q}{r^3}(\mathrm{i} kr -1) \exp(\mathrm{i} k r).$$
Here the dipole moment is written as ##q \vec{d} \exp(-\mathrm{i} \omega t)## and ##k=\omega/c##. The solution clearly shows that the sources are the oscillating charge-current distributions,
$$\rho(t,\vec{r}=-q \vec{d} \cdot \vec{\nabla} \delta(\vec{r}) \exp(-\mathrm{i} \omega t), \quad \vec{j}=-\mathrm{i} q \omega \vec{d} \delta^{(3)}(\vec{r}).$$
For ##k r=2 \pi r/\lambda \ll 1## we find a static electric dipole field which is oscillating synchronous and a magnetic field which oscillates with a relative phase shift of ##\pi/2## with the dipole:
$$\vec{E}'(\vec{r}) \simeq \frac{q}{4 \pi r^3} [3\hat{r} (\hat{r} \cdot \vec{d})-\vec{d}],$$
$$\vec{B}'(\vec{r}) \simeq \frac{\mathrm{i} k}{4 \pi r^2} q \hat{r} \times \vec{d}.$$
The near field goes like ##1/r^3## like a static electric dipole field.
For ##k r \gg 1## we find
$$\vec{E}'(\vec{r})=\frac{k^2}{2 \pi r} [\vec{d}-\hat{x}(\hat{r} \cdot \vec{d})] \exp(\mathrm{i} k r),$$
$$\vec{B'}(\vec{r})=\hat{r} \times \vec{E}'.$$
The far field is thus like a spherical wave going like ##1/r## with an amplitude modulated by the typical dipole characteristics.
Just one remark on Einstein causality:
That the near fields are synchronous with the dipole oscillations without retardation, however, must not be mistaken as indicating instantaneous action as a distance, but it's the near-field approximation of a stationary state, i.e., the here given solution is one, where the oscillation of the dipole was switched on asymptotically in the very far past, ##t_0 \rightarrow -\infty##. To get a solution for the case that the dipole oscillation was started at ##t=0## you have to use a Fourier transformation for the source,
$$\vec{j}(t,\vec{r})=-\mathrm{i} q \vec{d} \int_{\mathbb{R}} \frac{\mathrm{d} \omega}{2 \pi} A(\omega) \omega \exp(-\mathrm{i} \omega t),$$
where ##A(\omega)## is sufficiently quickly falling for ##\omega \rightarrow \pm \infty## and as an analytic function must have poles only in the lower complex ##\omega## plane. Due to the exponential in the Fourier integral one has to close the contour in the upper plane for ##t<0## and then you have ##\vec{j}(t,\vec{r})=0## for ##t<0##. Now the very same Fourier integration has to be done for the electromagnetic field, and doing this integral for the exact solution, including the spatial exponential ##\exp(\mathrm{i} k r)=\exp(\mathrm{i} \omega c r)## shows that the wave front propagates exactly with the speed of light everywhere, i.e., for ##kr-\omega t>0## the electromagnetic field is 0, i.e., there is no field earlier than "allowed" by the relativistic "speed limit".