Roroy
- 9
- 0
Hello,
I'm going through Kirchoff's second law, and stumbled across this example on this page:
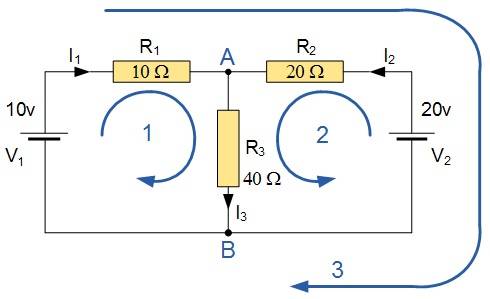
In the image above, you can see that the blue arrows (both arrow 1 and arrow 2) indicate the direction that the current goes in. However, I am wondering why the current cannot go as per the red and green arrows depicted in the image below?
What stops the electrons from going from Negative end of 10V battery to positive end of 20V battery (as per red arrow)? What stops them going from negative end of 20V to positive end of 10V (as per green arrow)?
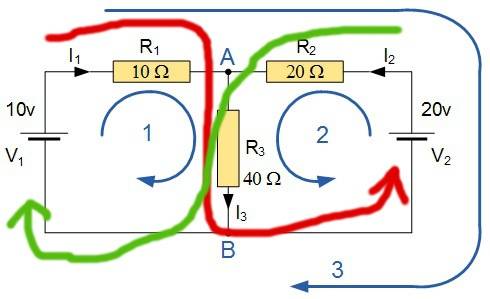
Any help much appreciated.
I'm going through Kirchoff's second law, and stumbled across this example on this page:
In the image above, you can see that the blue arrows (both arrow 1 and arrow 2) indicate the direction that the current goes in. However, I am wondering why the current cannot go as per the red and green arrows depicted in the image below?
What stops the electrons from going from Negative end of 10V battery to positive end of 20V battery (as per red arrow)? What stops them going from negative end of 20V to positive end of 10V (as per green arrow)?
Any help much appreciated.