clairez93
- 113
- 0
Homework Statement
A series of true/false questions. I guess I don't understand the concepts of this very well:
1. If you know the directional derivative of f(x,y) in two different directions at a point P, we can find the derivative with respect to the x and y axes and thus we can determine the derivatives at this point P.
2. If f(x,y) = x^{2} + y^{2} then
\nabla f\bot graph(f).
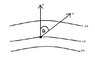
For the level curves in the figure and point P:
a) If u is a unit vector and the level curves of f(x,y) are given as shown, then at the point P, we have
f_{u} = D_{u}f = \nabla f.
b) For the same f and the unit vector v shown,
f_{v} = D_{v}f =(I can't get this to come out right, but it's supposed to say that the magnitude of the gradient of f times cos theta)
c) There is a function z = f(x,y) and a point P so that the maximum rate of change in f as you move away from P is 7 and the minimum rate of chang ein f as you move from P is -5.
Homework Equations
The Attempt at a Solution
1. Not sure about this, but I want to guess that it has something to do with the chain rule for many variables?
2. I want to say true, because I know that the gradient is always perpendicular to the level curve, but I'm not sure if that is what "graph(f)" refers to?
a) Not a clue really here. I want to say false because I don't think that the directional derivative is equal to the gradient, unless they're parallel? In any case I don't think that they would be equal to the partial derivative...
b) I kind of want to say false again because, because where did the unit vector go? The dot product of the gradient and the unit vector u should be equal to the directional derivative, but the u has disappeared, unless u is equal to 1? Which I don't think it is.
c) So they're trying to say that the magnitude of the gradient is 7 and the negative of that is -5? I think that's wrong, because isn't the maximum and minimum the same except that the minimum is the negative of the magnitude? So it can't be 7 and -5?
Most of my answers here are complete guesswork. Help would be appreciated.
Attachments
Last edited: