Dispersion relation for diatomic linear chain.

[Wminus]

Hi. Here's the dispersion relation for a diatomic linear chain, where the distance is a/2 between each atom.

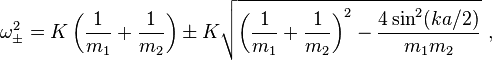
My issue here is that if you set m_1=m_2=m, i.e. set both atoms equal to each other, it doesn't automatically reduce to the old acoustic dispersion relation as the ± term doesn't disappear.

What's up with that?

 

[Wminus]

BTW, I got the dispersion relation from here http://en.wikipedia.org/wiki/Phonon#Dispersion_relation

 

[DrDu]

I can't see any problem. Maybe you should fresh up your knowledge of the trigonometric equations?

 

[Wminus]

I can't see any problem. Maybe you should fresh up your knowledge of the trigonometric equations?

OK, sorry I should've written everything out in details in the OP. My problem is that the plus-minus sign is being problematic. It gives two solutions that are phase-shifted with regards to each other. Setting the masses equal, the equation from OP reduces to:

$\omega^2 = K(2/m) \pm K \sqrt{(2/m)^2 - (2/m)^2 sin^2{ka/2}} = \frac{2K}{m}(1 \pm cos(ka/2)) \Rightarrow \omega_+ = \sqrt{\frac{4K}{m}} |cos(ka/4)|$ & $\omega_- = \sqrt{\frac{4K}{m}} |sin(ka/4)|$.

How do I get rid of the $\omega_+$ term, the optical mode? Which physical argument makes it invalid?

 

[DrDu]

They are both correct. Note that your basis contains two atoms and not just one, so that a is different.

 

[Wminus]

They are both correct. Note that your basis contains two atoms and not just one, so that a is different.

If you graph both of them in a diagram, you get a dispersion relation with 2 modes! This is supposed to be impossible, isn't it?

 

[DrDu]

No, it isn't. You have a basis with two atoms, so you get two modes, an acoustic one and an optical one. However, when the two atoms become identical, the two curves will touch at the zone boundaries.
Do you know the difference between a reduced and an extended zone scheme? Here it is for the example of a quasi-free electron:
http://www.pha.jhu.edu/~jeffwass/2ndYrSem/pics/Slide19.JPG

 

[Wminus]

I think I do, yes. But in the case of a single-atom chain there should be only one mode regardless of what basis or zone scheme you choose. Right?

 

[Wminus]

I mean, the two-atom chain with masses m_1 and m_2 should turn into a standard single-atom chain if we set m_1=m_2=m. So the dispersion relation should go from just one mode to two, right?

 

[DrDu]

It doesn't because you chose to describe it using a lattice with a cell containing two atoms instead of one. Given N atoms for a whole crystal, you can describe it in terms of either N k-values forming one band or N/2 k-values forming two bands.

 

[Wminus]

It doesn't because you chose to describe it using a lattice with a cell containing two atoms instead of one. Given N atoms for a whole crystal, you can describe it in terms of either N k-values forming one band or N/2 k-values forming two bands.

I think I get all of this now. It's got to do with the reduced/extended scheme ways of viewing the dispersion relation. thanks.