- #1
thatguy14
- 45
- 0
Homework Statement
In deriving the formula
div v = [itex]\frac{∂v_{x}}{∂x}[/itex] + [itex]\frac{∂v_{y}}{∂y}[/itex] + [itex]\frac{∂v_{z}}{∂z}[/itex]
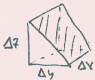
we used a rectangular solid infinitesimal volume; however, any shape will do (although the calculation gets harder). To see an example, derive the same formula using the prism-shaped volume shown (figure attached). This could be a volume element next to an irregular surface.
Homework Equations
Definition of divergence
div v = lim Δτ→0 [itex]\frac{\int v \cdot da}{Δτ}[/itex] where Δτ = small volume and the integral is a over a closed surface bound Δτ
The Attempt at a Solution
So I am having some issue with this question. A thing to note is that we are approximating the integral as just v[itex]\circ[/itex]da where v is at some point on the surface. This is due to it being an infinitesimal volume.
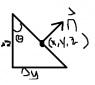
The main problem I am having is I think I am making a mistake on the top face somehow. If you look at figure 2 which is my crude drawing to represent n it is then
n = (cos[itex]\theta[/itex] jhat + sin[itex]\theta[/itex] khat)
So then for the top face if h = the slanted side
da = hΔx(cos[itex]\theta[/itex] jhat + sin[itex]\theta[/itex] khat)
=Δx(Δz jhat + Δy khat) because h can be expressed in terms of sin and cos of the other sides.
so then v dot da = v[itex]_{y}[/itex](x, y, z)ΔxΔz + v[itex]_{z}[/itex](x,y,z)ΔxΔy
hopefully so far so good. Now for the other faces
bottom
da = ΔxΔy (-khat direction)
v dot da = -v[itex]_{z}[/itex](x, y, z-[itex]\frac{1}{2}[/itex]Δz)ΔxΔy
back(zx plane)
da = ΔxΔz
v dot da = -v[itex]_{y}[/itex](x, y-[itex]\frac{1}{2}[/itex]Δy, z)ΔxΔz
so then when I put it all together and divide by Δτ = [itex]\frac{1}{2}[/itex]ΔxΔyΔz
it almost looks like the definition of a derivative except I am left with a 1/2. What did I miss? Any help would be greatly appreciated and if you need me to clarify let me know.