BayMax
- 4
- 3
- Homework Statement
- equations of motion
- Relevant Equations
- angular momentum equation
I need help to understand this problem taken from Mechanical Vibrations by S. Rao
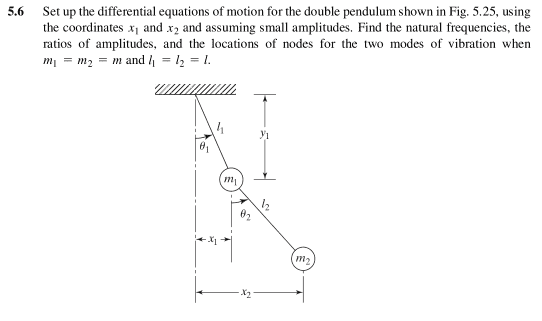

I know that the equations of motion could be obtained in various ways, for example using the Lagrangian, but, at the moment, I am interested in understanding the method he used. In particular, if I'm not mistaken, he used moments equilibrium about point O and point ##m_1##. Here's my questions:
1- Why in the moments equilibrium about the point O (equation E1) he considered only the forces acting on ##m_1## as if ##m_2## were not there and also just the moment of inertia of ##m_1##?
2- But above all, in the equation E2, where does the highlighted term ##m_2⋅l_2(l_1⋅\ddot\theta_1)## come from and what does it represent?
3- I have a lot of problems when I'm asked to find equations of motion of a system of particles (like in this case) or of a rigid body, so I need some good resources (textbooks preferably) where I can find all the tools I need to understand and solve this kind of problems.
Thanks !
I know that the equations of motion could be obtained in various ways, for example using the Lagrangian, but, at the moment, I am interested in understanding the method he used. In particular, if I'm not mistaken, he used moments equilibrium about point O and point ##m_1##. Here's my questions:
1- Why in the moments equilibrium about the point O (equation E1) he considered only the forces acting on ##m_1## as if ##m_2## were not there and also just the moment of inertia of ##m_1##?
2- But above all, in the equation E2, where does the highlighted term ##m_2⋅l_2(l_1⋅\ddot\theta_1)## come from and what does it represent?
3- I have a lot of problems when I'm asked to find equations of motion of a system of particles (like in this case) or of a rigid body, so I need some good resources (textbooks preferably) where I can find all the tools I need to understand and solve this kind of problems.
Thanks !