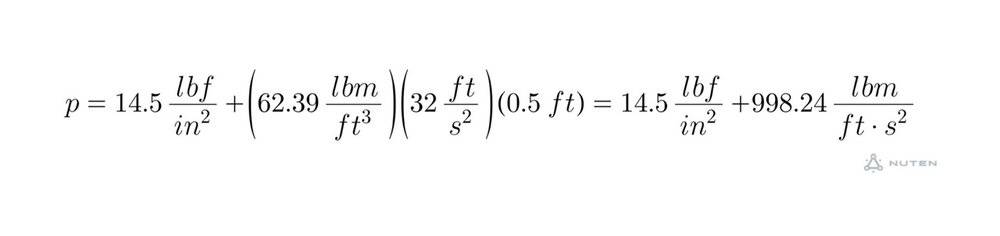cwill53
- 220
- 40
- Homework Statement
- A vacuum gage at the intake duct to a fan gives a reading of 6 in of water. The surrounding atmospheric pressure is ##14.5 lbf/in^2## Determine the absolute pressure inside the duct, in ##lbf/in^2.## The density of water is ##62.39lb/ft^3##, and acceleration of gravity is ##32.0 ft/s^2##.
- Relevant Equations
- $$p=p_{atm}+ \rho gL$$
These units complicate everything and I simply cannot get them to check out for the life of me. After making some conversions I got to this point: