judas_priest said:
Thank you for your great explanation!
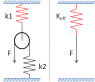
I still haven't understood why force F applied on k2 translates to 2F on k1
Once Force F is applied, the tension in the string means both sides of the pulley are pulled down with force F - giving a total of 2F
judas_priest said:
Also, solving it your way gives me
(2k<sub>1</sub>k<sub>2</sub>)/(2k<sub>2</sub> + k<sub>1</sub>)
Is that right?
I can't be certain that is right - I have never actually found the answer - that was always up to you, but it has a chance if it passes the "extremes" testing. [that was an earlier post of mine].
If K1 is very large (the spring is very stiff) it may be considered to be just a piece of string.
When you apply a force, the pulley stays put, and the system is effectively just a single spring, K2
In your answer, the denominator 2k
2 + k
1 is effectively just k
1 as this value renders 2k
2 insignificant.
The expression is thus
(2k<sub>1</sub>k<sub>2</sub>)/(k<sub>1</sub>)
which simplifies to 2k
2
Pity about that leading 2
If instead K2 is very large (that spring is very stiff), then K2 can be replaced with a piece of string - and the mechanical advantage of the pulley means the effective spring constant is K1/2.
when K2 >> K1, 2k
2 + k
1 is effectively just 2k
2
he expression is thus
(2k<sub>1</sub>k<sub>2</sub>)/(2k<sub>2</sub>)
which simplifies to k
1
Where has the half gone??
It would be good if there was not a 2 in the numerator of your answer??
WIthout seeing your step by step derivation, I cannot see where (if at all) you have gone wrong.