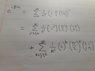Eigenvectors of exponential matrix (pauli matrix)

[Punctualchappo]

Homework Statement

Find the eigenvectors and eigenvalues of exp(iπσ_x/2) where σ_x is the x pauli matrix:
10
01

Homework Equations

I know that σ_xⁿ = σ_x for odd n
I also know that σ_xⁿ is for even n:
01
10

I also know that the exponential of a matrix is defined as Σ(1/n!)xⁿ where the sum runs from n=0 to infinity

The Attempt at a Solution

Using knowledge of the matrix exponential, I can say that exp(iπσ_x/2) = Σ(1/n!)(iπσ_x/2)ⁿ. I can then split this into two sums, one for even n and one for odd n. This allows me to take the power off the matrices for easier summing. It's then that I get stuck. I've attached a file showing the two sums because it's easier and clearer to show you this way.[/B]

I'd really appreciate any help that can be given.

 

[Punctualchappo]

I've realized that when written as the two sums, it's clear that there are only two linearly independent eigenvectors for each sum. I'm not sure how it works when the i's get multiplied in though. Aren't there infinite eigenvalues to reflect the infinite nature of the sums?

 

[BvU]

Hi chap, welcome to PF :),

What would an eigenvector of exp(iπσ_x/2) look like ? What conditions would it have to satisfy ?

And what about eigenvectors of σ_x itself ?

 

[Punctualchappo]

So the eigenvectors would have to satisfy exp(iπσ_x/2)v = Av where A is the eigenvalue. I know that eigenvectors of σ_x are (1,1) and (1,-1)
Thanks for your help.