Electric circuit & missing resistance/voltage

AI Thread Summary
To solve for the missing resistances, currents, and voltages in the circuit, it is crucial to apply Ohm's Law (V = IR) and understand the behavior of resistors in parallel. R3 and R4, being in parallel with R2, will indeed have the same voltage across them, which is confirmed to be 1.2 V. This means that the total voltage across R3 and R4 is also 1.2 V. The relationship between the resistances can be further analyzed using the equations R = V/I and I = V/R. Understanding these principles will help in determining the unknown values in the circuit.
pebbles3
Messages
9
Reaction score
0

Homework Statement


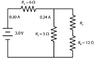
I'm supposed to find the missing resistances, currents, and voltages from the first picture (attached)

Homework Equations


v = IR
R = V/I
I=V/R

The Attempt at a Solution


My attempt is in the second attached picture. I'm completely lost on what to do for R3. Would R3 and R4 have the same voltage? I'd really appreciate some help with this.
 

Attachments

  • diagram1.png
    diagram1.png
    2.5 KB · Views: 428
  • diagram2.png
    diagram2.png
    3.3 KB · Views: 443
Physics news on Phys.org
Anyone?
 
R3+R4 is in parallel with R2. What does that tell you about the total voltage across R3+R4?
 
The voltages are the same in parallel, right? So.. would the total voltage across R3+R4 equal 1.2 V?
 
pebbles3 said:
The voltages are the same in parallel, right? So.. would the total voltage across R3+R4 equal 1.2 V?

Yes, of course.
 
  • Like
Likes 1 person
Thread 'Collision of a bullet on a rod-string system: query'

Thread 'Collision of a bullet on a rod-string system: query'

In this question, I have a question. I am NOT trying to solve it, but it is just a conceptual question. Consider the point on the rod, which connects the string and the rod. My question: just before and after the collision, is ANGULAR momentum CONSERVED about this point? Lets call the point which connects the string and rod as P. Why am I asking this? : it is clear from the scenario that the point of concern, which connects the string and the rod, moves in a circular path due to the string...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Solving series-parallel circuits
Replies
1
Views
1K
Equivalent resistance of a circuit
Replies
3
Views
2K
Reading of Ammeter for this circuit with Voltage Controlled Resistors
Replies
9
Views
1K
Understanding example in Wikipedia entry for open circuit voltage
Replies
3
Views
2K
Write boolean expression describing this circuit
Replies
4
Views
971
A circuit involving two non-linear resistances (incandescent lamps)
Replies
14
Views
2K
Determine the Thevenin equivalent circuit
Replies
2
Views
2K
FInding current in parallel and series circuits
Replies
10
Views
3K
Current through a circuit when the key is open
Replies
42
Views
5K
Identical Batteries in Parallel do not Draw Same Current, Non-Ideal?
Replies
7
Views
830

Hot Threads

Recent Insights

Back
Top