Electric field and potential of a charged disc

[carllacan]

Homework Statement

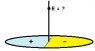
Calculate the electric field on axis of a disc that has charge +q on one half and -q on the other.

Describe the behavior of the potential along the same axis at points far from the disc.

Homework Equations

The Attempt at a Solution

My intuition says its zero, as for every contribution to E from one part there will be one at the samne distant but of opposite sign (in both the horizontal and vertical components) that will cancel it. I've done the math and I've also got zero.

The problem is that I'm later asked to describe the behavior of the potential on the disc, and it feels weird that the answer is simply 0.

Please tell me if my intuition is right and if not Ill post my math to see where have I had a mistake.

Thank you for reading.

 

[TSny]

If the setup is as shown below, then E would not be zero on the axis.

 

[carllacan]

Ok, I was not enterely sure my intuition, but my math told me the same
$\vec E(\vec r) = k \int \frac{dq}{R^3} \vec R = k \int \frac{\sigma' dS}{\rho ^2 +z^2) ^{3/2}} \vec{r}= k \int \frac{\sigma' \rho d \rho d\theta}{\rho ^2 +z^2) ^{3/2}} (x, y, z)$We separate the integral in two, one from $\theta = 0$ to $\theta = \pi$ , where $\sigma' = +\sigma$ and one from $\theta = \pi$ to $\theta = 2\pi$ , where $\sigma' = -\sigma$.
$k \int_{0}^{a} d\rho \int_{0}^{\pi} d\theta \frac{\sigma\rho }{(\rho ^2 + z ^2)^{3/2}}\vec{r} + k \int_{0}^{a} d\rho \int_{\pi}^{2\pi} d\theta \frac{-\sigma\rho }{(\rho ^2 + z ^2)^{3/2}}\vec{r}$

Now we write $\vec{r}$ as $(x\vec{i}+z\vec{k})$, since if we set the line where the charge changes to lie in the y-axis then the contributions from y < 0 will cancel those from y > 0.
$k \int_{0}^{a} d\rho \int_{0}^{\pi} d\theta \frac{\sigma\rho }{(\rho ^2 + z ^2)^{3/2}}(x\vec{i}+z\vec{k}) + k \int_{0}^{a} d\rho \int_{\pi}^{2\pi} d\theta \frac{-\sigma\rho }{(\rho ^2 + z ^2)^{3/2}}(x\vec{i}+z\vec{k})$

$k \int_{0}^{a} d\rho \int_{0}^{\pi} d\theta \frac{\sigma\rho }{(\rho ^2 + z ^2)^{3/2}} x\vec{i} + k \int_{0}^{a} d\rho \int_{0}^{\pi} d\theta \frac{\sigma\rho }{(\rho ^2 + z ^2)^{3/2}} z\vec{k} + k \int_{0}^{a} d\rho \int_{\pi}^{2\pi} d\theta \frac{-\sigma\rho }{(\rho ^2 + z ^2)^{3/2}} x\vec{i}+ k \int_{0}^{a} d\rho \int_{\pi}^{2\pi} d\theta \frac{-\sigma\rho }{(\rho ^2 + z^2)^{3/2}} z\vec{k}$

Changing $x$ for $\rho cos \theta$:
$k \int_{0}^{a} d\rho \int_{0}^{\pi} d\theta \frac{\sigma\rho }{(\rho ^2 + z ^2)^{3/2}} \rho cos \theta\vec{i} + k \int_{0}^{a} d\rho \int_{0}^{\pi} d\theta \frac{\sigma\rho }{(\rho ^2 + z ^2)^{3/2}} z\vec{k} + k \int_{0}^{a} d\rho \int_{\pi}^{2\pi} d\theta \frac{-\sigma\rho }{(\rho ^2 + z ^2)^{3/2}} \rho cos \theta \vec{i}+ k \int_{0}^{a} d\rho \int_{\pi}^{2\pi} d\theta \frac{-\sigma\rho }{(\rho ^2 + z^2)^{3/2}} z\vec{k}$
But now, if we integrate for $\theta$ we get 0!

 

[BvU]

May I remind you that you want to calculate $\vec E\;(\vec r)$, not $E(\vec r)$.
Since you only want to know it on the axis, this may well reduce to $\vec E(z)$, but it's still a vector: it has 3 components, which may be zero or not.

 

[carllacan]

May I remind you that you want to calculate $\vec E\;(\vec r)$, not $E(\vec r)$.
Since you only want to know it on the axis, this may well reduce to $\vec E(z)$, but it's still a vector: it has 3 components, which may be zero or not.

Yes, I see the mistake in my intuition now. I still get zero when I do the math, though.

 

[TSny]

It looks like you have it set up correctly. How are you getting the x-component integrations to be zero?

 

[carllacan]

When I integrate the $cos \theta$ I get $sin \theta$, which evaluated from 0 to $\pi$ and from $2\pi$ to $2\pi$ gives zero.

 

[BvU]

the contributions from y < 0 will cancel those from y > 0

Even though the $\sigma$ changes sign ?

:)

 

[TSny]

When I integrate the $cos \theta$ I get $sin \theta$, which evaluated from 0 to $\pi$ and from $2\pi$ to $2\pi$ gives zero.

Earlier you were integrating sinθ rather than cosθ. If you are now integrating cosθ, what should be the limits of integration for θ?

 

[carllacan]

Earlier you were integrating sinθ rather than cosθ. If you are now integrating cosθ, what should be the limits of integration for θ?

Yeah sorry, I miscopied that part and edited it later. It should be from 0 to $\pi$ and from $\pi$ to $2\pi$, so, if I'm not wrong
$\int_{0}^{\pi}d\theta cos\theta = [sin \theta ]_{0}^{\pi} = [sin \pi - sin 0] = 0$
$\int_{\pi}^{2\pi}d\theta cos\theta = [sin \theta ]_{\pi}^{2\pi} = [sin 2\pi - sin \pi] = 0$

 

[carllacan]

Even though the $\sigma$ changes sign ?

:)

I placed the dividing line along the y axis, so i think sigma doesn't change as you go from y<0 to y>0

Thank you, though :-)

 

[TSny]

Yeah sorry, I miscopied that part and edited it later. It should be from 0 to $\pi$ and from $\pi$ to $2\pi$, so, if I'm not wrong
$\int_{0}^{\pi}d\theta cos\theta = [sin \theta ]_{0}^{\pi} = [sin \pi - sin 0] = 0$
$\int_{\pi}^{2\pi}d\theta cos\theta = [sin \theta ]_{\pi}^{2\pi} = [sin 2\pi - sin \pi] = 0$

OK, I think we're getting to the problem. I don't believe your limits of integration are correct. You have x = ρ cosθ. If θ varies from 0 to π, will x vary over the correct domain?

 

[BvU]

I placed the dividing line along the y axis, so i think sigma doesn't change as you go from y<0 to y>0

Thank you, though :)

I see. So did TS and we all agree that a clear drawing could have prevented this mistake. Something to remember for next time.

all variables and given/known data

 

[carllacan]

I see. So did TS and we all agree that a clear drawing could have prevented this mistake. Something to remember for next time.

I thought the written comment would be enough. My apologies. I'll ad one now.

OK, I think we're getting to the problem. I don't believe your limits of integration are correct. You have x = ρ cosθ. If θ varies from 0 to π, will x vary over the correct domain?

Yes, that was it. Infinite thanks for you sir! The way I had done it my $\theta$ was sweeping from a positive quarter and a negative quarter on each integral.

Ok. so my new approach is like this:
https://photos-5.dropbox.com/t/2/AAChv5_j_8NbxAWSbmVsD57BADEhas7c2KOzcASEDJWhPw/12/28182931/png/1024x768/3/1421877600/0/2/disc.png/CJOTuA0gAyACIAEoAigB/vRUpN25j73rui7xiAEK6rt3FaIO9P7Tf705qjtnWPOY

Now the vector component that will get canceled is x, the $y$ is $\rho sin\theta$, which doesn't cancel when integrating, and I get an electric field in the direction of y. I have no way of checking that it is the right solution, but if there's any mistake it will be minor, I suppose.

Thank you all for your time. Its been a while since my last time here, where has the "Thank" buttons gone?

 

[BvU]

Nice picture. This way $\theta$ bounds make good sense. (Confession: I had this picture in mind from the choice of bounds; didn't look all that closely to the expressions. Goes to show how brainwashed one is after so many years...).

Anyway, the buttons are now more in the facebook spirit.

And you do have a kind of check: the charge distribution has dipole character, so the field should have that too. Nice feature of the exercise: they ask for that in the second part.

 

[carllacan]

I have a similar problem in the second part:
$\phi(\vec r) = k \int \frac{dq}{R} = k \int \frac{\sigma ' dS}{R} = k \int \frac{\sigma' \rho }{R}d\rho d\theta =$
$k \int _{0} ^{a} d\rho \int _{0} ^{\pi} d\theta \frac{\sigma \rho}{(\rho^2 + z^2)^{1/2}}- k \int _{0} ^{a} d\rho \int _{\pi} ^{2\pi} d\theta \frac{\sigma \rho}{(\rho^2 + z^2)^{1/2}} =$
$k \int _{0} ^{a} d\rho \frac{\sigma \rho}{(\rho^2 + z^2)^{1/2}}[\theta]_{0} ^{\pi}- k \int _{0} ^{a} d\rho \int _{\pi} ^{2\pi} d\theta \frac{\sigma \rho}{(\rho^2 + z^2)^{1/2}}[\theta]_{\pi} ^{2\pi} =$
$k \int _{0} ^{a} d\rho \frac{\sigma \rho}{(\rho^2 + z^2)^{1/2}}[\pi]- k \int _{0} ^{a} d\rho \int _{\pi} ^{2\pi} d\theta \frac{\sigma \rho}{(\rho^2 + z^2)^{1/2}}[\pi] = 0$

What am I missing now?

 

[BvU]

What do you expect the potential to be ?

 

[BvU]

The E field is more interesting to inspect. It should be similar to this for z >> R . Gives you a chance to compare a/R to what you expect for the center of gravity (cq charge) of a half-disc