Aaryan34532
- 10
- 1
- Homework Statement
- If a positively charged particle follows a circular path as shown below what will the electric field be out of the options below.
- Relevant Equations
- No equations. this is supposedly intuition.
Here is picture. Answers is A.
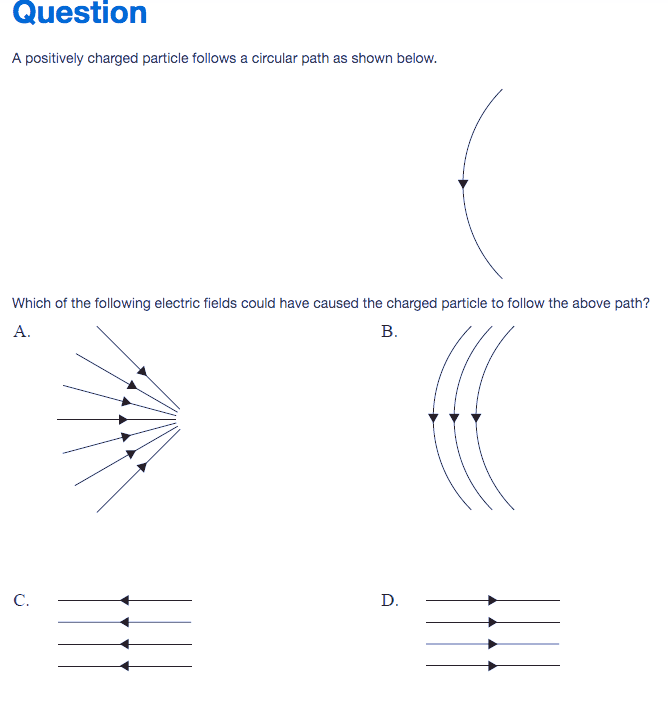 My attempt was that I thought if i were to place a positive test charge then it would go from top to bottom if there was a positive charge in the center it was avoiding and a positively charged particle at the top, but an electron at the bottom so it would avoid the positively charged particles and head for the electron thus the electric field would look like B and that's exactly how a positively charged particle would also do so.
My attempt was that I thought if i were to place a positive test charge then it would go from top to bottom if there was a positive charge in the center it was avoiding and a positively charged particle at the top, but an electron at the bottom so it would avoid the positively charged particles and head for the electron thus the electric field would look like B and that's exactly how a positively charged particle would also do so.
But then the answer was A and i got thinking to how in circular motion there is centripetal force towards center, but honestly since this is electric fields i feel weird to correlate these and don't feel so correct.
But then the answer was A and i got thinking to how in circular motion there is centripetal force towards center, but honestly since this is electric fields i feel weird to correlate these and don't feel so correct.