Electric Field of a Point Charge and Thin Ring: A Comparative Analysis

[Physicslearner500039]

Homework Statement

A point charge q is located at the center of a thin ring of radius R with uniformly distributed charge —q. Find the magnitude of the electric field strength vector at the point lying on the axis of the ring at a distance x from its center, if x » R.

Relevant Equations

NA

I thought it was easy but i am not getting the correct answer

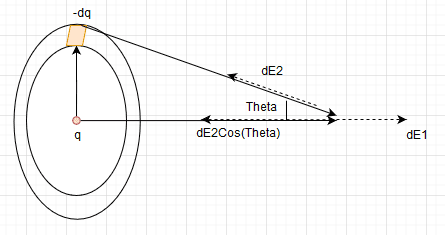
The electric field due the point charge q is
$E1 = q/(4\pi\epsilon x^2)$
The electric field due to the thin ring of radius R is considering the electric field due to the element charge dq (dS)
$dE2 = dq/4\pi\epsilon (x^2 + R^2) \\ dE2 = \lambda * dS/(4\pi\epsilon (x^2 + R^2)) \\ dE2_{net} = dE2\cos{\theta} \\ dE2_{net} = \lambda * dS * \cos{\theta} /(4\pi\epsilon (x^2 + R^2)) \\ \cos\theta = x/(x^2 + R^2)^\frac 1 2 \\ \lambda * dS * x /(4\pi\epsilon (x^2 + R^2)^ \frac 3 2) \\ \int_0^{2\pi R} \lambda dSx/(4\pi\epsilon (x^2 + R^2)^ \frac 3 2) \\ \lambda x/(4\pi\epsilon (x^2 + R^2)^ \frac 3 2)\int_0^{2\pi R} dS\\ \lambda x 2\pi R/(4\pi\epsilon (x^2 + R^2)^ \frac 3 2) \\ E2_{net} = qx/(4\pi\epsilon (x^2 + R^2)^ \frac 3 2) \\$
The net field is
$E2_{net} - E1 = qx/(4\pi\epsilon (x^2 + R^2)^ \frac 3 2) - q/(4\pi\epsilon x^2)$
For $x > R$ the net field is 0.

 

[etotheipi]

The net field is
$E2_{net} - E1 = qx/(4\pi\epsilon (x^2 + R^2)^ \frac 3 2) - q/(4\pi\epsilon x^2)$
For $x > R$ the net field is 0.

Your expression looks fine to me, note that you don't even need to substitute in the linear density; since all charge elements $dq$ on the ring are identical, you can just integrate up the $dq$'s from 0 to $-q$.

However I think you've jumped the gun a bit on the $x\gg R$ case. It might well turn out to be true, however can you think of any other way of simplifying that net field expression if $\frac{R}{x}$ is small? Especially the bit with the $(x^2 + R^2)^{-\frac{3}{2}}$?

 

[Delta2]

However I think you've jumped the gun a bit on the $x\gg R$ case. It might well turn out to be true, however can you think of any other way of simplifying that net field expression if $\frac{R}{x}$ is small? Especially the bit with the $(x^2 + R^2)^{-\frac{3}{2}}$?

The way I see it is indeed approximately zero for x>>R, because if we factor out $x^2$ from the denominator of the first term and then set $\frac{R^2}{x^2}\approx 0$ we get also zero for the net electric field.

Besides that's a nice corollary from Jeffimenko's equations, using the approximation $\frac{1}{|\vec{r}-\vec{r'}|}=\frac{1}{|\vec{r}|}$( which is valid for vector $\vec{r}$ such that it is much bigger in magnitude than the vector $\vec{r'}$ which spans the source space, which in simple words means for points far away from the source such that the distance from the source is much bigger than the dimensions of the source), we conclude that the source behaves approximately as a point source with charge equal to the total charge of the source.

 

[etotheipi]

My approach was to rewrite it as $$E_x = kqx^{-2}(1+\frac{R^2}{x^2})^{-\frac{3}{2}} - kqx^{-2}$$ and then you can do a binomial expansion to the first order in $\frac{R^2}{x^2}$, which gives you a sort of nice expression in one single fraction.

I won't spoil the expression for the OP, but I do agree that it approaches zero.

Besides that's a nice corollary from Jeffimenko's equations, using the approximation $\frac{1}{|\vec{r}-\vec{r'}|}=\frac{1}{|\vec{r}|}$( which is valid for vector $\vec{r}$ such that it is much bigger in magnitude than the vector $\vec{r'}$ which spans the source space, which in simple words means for points far away from the source such that the distance from the source is much bigger than the dimensions of the source), we conclude that the source behaves approximately as a point charge with total charge the total charge of the source.

Interesting! I'd never heard of that set of equations, but that is indeed consistent with what we got so is a nice extension! Thanks for sharing that, I've got a bit of reading to do this evening now