vladimir69
- 124
- 0
Homework Statement
A thin piece of wire, with charge per unit length \lambda lies on the x-axis and extends from x=-L/2 to x=+L/2 so that it has a length L. Show that the electric field (at the point (x,y) = (0,D)) in the +y-direction has magnitude given by 2\frac{\lambda k_{e}}{D}\sin(\theta_{0}).
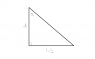
The file attached below is to show where theta is pulled from.
Homework Equations
d\mathbf{E}=k_{e}\frac{dq}{r^2}\mathbf{\hat{r}}
The Attempt at a Solution
Here is what I managed to boil up
First let
\theta+\phi=\frac{\pi}{2}
then
r=\frac{D}{\sin(\phi)}
dq=\lambda dx = -\lambda D d\phi
\hat{r}=\left(\begin{array}{cc}\cos(\phi)\\\sin(\phi)\end{array}\right)
\int dE_{y}=-\frac{\lambda k_{e}}{D}\int_{\phi_{0}+\frac{\pi}{2}}^{\theta_{0}-\frac{\pi}{2}}\sin^3(\theta)d\theta
Finally
E_{y}=\frac{\lambda k_{e}}{D}(2\sin(\theta_{0})-\frac{2}{3}\sin^3(\theta_{0}))
Did I do something wrong or did they assume that the sin cubed term is small and hence got rid of it?
Thanks,