- #1
brojas7
- 20
- 0
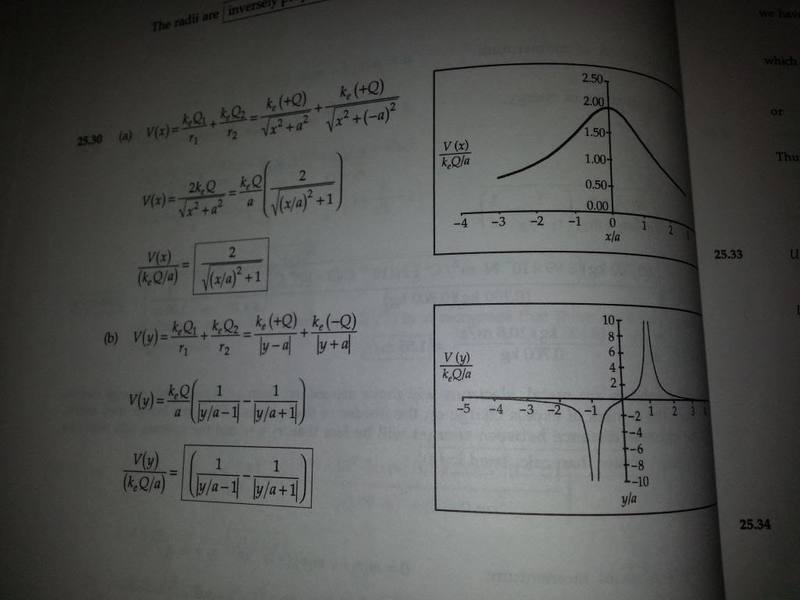
Two charged particles of equal magnitude are located along the y-axis equal distances above and below the x-axis.
Plot a graph of the electric potential at points along the x-axis over the interval -3a<x<3a. You should plot the potential in units of (KeQ)/a
Let the charge of the particle located at y=-a be negative. Plot the potential along the y-axis over the interval -4a<y<4a.
I was able to do :
(KeQ1)/r^2 + (KeQ2)/r^2 =
(KeQ)/ sqrt(x^2 + a^2) + (KeQ)/ sqrt(x^2 + -a^2) =
(2KeQ)/ sqrt(x^2 + -a^2)
Why did they factor out a KeQ/a, was it necessary? how do you plug in x to get the graph if you don't know 'a'.
and for the y axis, why did they get an absolute value for y-a and y+a.
ANSWER:
Plot a graph of the electric potential at points along the x-axis over the interval -3a<x<3a. You should plot the potential in units of (KeQ)/a
Let the charge of the particle located at y=-a be negative. Plot the potential along the y-axis over the interval -4a<y<4a.
I was able to do :
(KeQ1)/r^2 + (KeQ2)/r^2 =
(KeQ)/ sqrt(x^2 + a^2) + (KeQ)/ sqrt(x^2 + -a^2) =
(2KeQ)/ sqrt(x^2 + -a^2)
Why did they factor out a KeQ/a, was it necessary? how do you plug in x to get the graph if you don't know 'a'.
and for the y axis, why did they get an absolute value for y-a and y+a.
ANSWER:
