Electric Potential Over Non-Uniform Rod

[Haptic9504]

Homework Statement

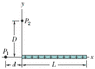
The thin plastic rod shown in the figure has length L = 18.0 cm and a nonuniform linear charge density λ = cx, where c = 14.5 pC/m2. With V = 0 at infinity, find the electric potential at point P1 on the axis, at distance d = 5.10 cm from one end.

Figure is attached.

Homework Equations

$$q= \lambda x \\ \lambda = cx \\ dv = (kdq)/r$$

The Attempt at a Solution

$$q= \lambda x \\ dq = \lambda dx \\ dq = cxdx$$

I figured you would just use
$$v =kc \int_{0}^{L}[x/(x+d)]dx$$
And plug in L, solving for V, in which I get -0.17V, which is flagged as incorrect.

Am I approaching this correctly or is there something I am missing?

 

[gneill]

The setup for the integral looks okay. You'll have to show details of how you solved the integral.

 

[Haptic9504]

This can be closed, I just integrated incorrectly.