- #1
Samson4
- 245
- 15
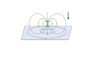
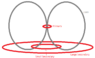
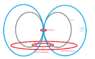
In the situation of a magnet moving towards a flat sheet of copper; why doesn't the copper gain angular moment as the electrons move in concetric circles? The electrons are experiencing friction as they move through the copper.