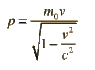Electrons subjected to a continuous force

[abotiz]

Hi there!

I got some difficulty understanding a question regarding electrons


Electrons which are initially at rest are subjected to a continuous force of 2E-12 N
along a length of 2 miles and reach very near the speed of light.

a) Determine how much time is required to increase the electrons speed from 0.93c to 99c

b) Approximately how far does the electron go in this time? What is approximate about your result?

Because the book don't offer any answers I feel unsure about my answer that follows;

The Impuls = mv1-mv0 Where m is the electrons mass ( 9.109 E-31) and v1=0.99C and v0=0.93C

So I get the Impuls, and then I= F*t I divide the Impuls with the force ( 2E-12) and get the time 8.19E-12 is this right?

And b) I use vt=s where v is 0.99C and get the length 2.43E-3

Have a made a mistake somewhere? Also, I don't understand the second question in b) " What is approximate about your result? "


Thank you

 

[Hootenanny]

You're answer varies from the books because your applying classical mechanics to a relativistic particle.

Try using relativistic mechanics.

 

[abotiz]

Thanks for your reply!

Okay, so I should be using this instead?

If I do, I get the time 2.767E-11 s

And the meters it travels would be 0.016 m ( here I used (0.93c+0.99c) multiplied with the time, is this right or should I just have 0.99c)